Второй взгляд: цепи и антицепи

—1.5—

Изложение этого параграфа частично украдено из статьи А. Спивака в “Кванте”.

Начнём с такой модельной задачи.

Король сказочной страны пригласил на пир всех людоедов своей страны. Среди них есть людоеды, которые хотят съесть других людоедов. Известно, что наидлиннейшая цепочка, в которой первый людоед хочет съесть второго, второй —- третьего, и так далее, состоит из $m$ людоедов. Докажите, что король может так рассадить людоедов за $m$ столов, что ни за каким столом никто не будет хотеть съесть никого из сидящих за тем же столом.

Людоед из мультфильма Э. Назарова 'Людоед и принцесса', 1977 г.

Решение. Замоделируем людоедов вершинами графа, а ориентированное ребро $A \to B$ проведём если людоед $A$ хочет съесть людоеда $B$.
Условие задачи исключает (ориентированные) циклы в этом графе, иначе есть бесконечная цепочка гастрономических предпочтений. Отсюда следует, что существуют некровожадные людоеды – те, которые не хотят съесть никого. Действительно, если в конечном графе из каждой вершины выходит хотя бы одна стрелка, то стартуя из произвольной вершины и переходя по стрелкам, мы вынужденно найдём цикл.

Итак, в графе есть по крайней мере одна вершина-сток, т.е. вершина без исходящих стрелок. Посадим всех таких мирных людоедов за стол №1, и выбросим их из нашего графа (разумеется, со всеми инцидентными стрелками). Теперь повторим тот же аргумент: в новом выберем все вершины без исходящих стрелок (они есть), и посадим их за стол №2. Почему не возникнет конфликта? Если за столом №2 сидят людоеды $A$ и $B$ такие что $A \to B$, тогда у вершины $A$ была исходящая стрелка в (урезанном) графе, и его не должны были выбирать на шаге 2. Далее мы повторяем то же, что и раньше: на $i$-ом шаге мы выбрасываем из графа всех людоедов, которые уже посажены за столы с номерами $<i$, в оставшемся графе выбираем все вершины без исходящих стрелок, и сажаем их за стол №$i$.

Рассадка людоедов

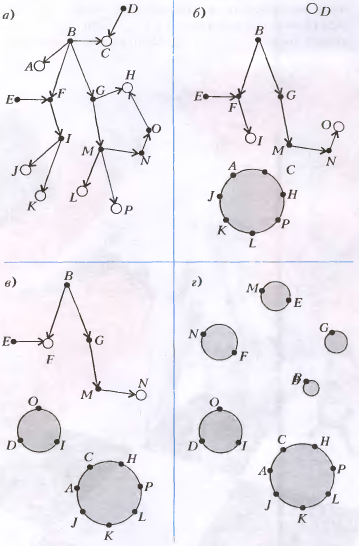
Ясно, что процесс закончится вместе с тем как закончатся людоеды в графе. Вопрос, на который нам нужно ответить: почему процесс закончится за $m$ шагов? Для этого нужно провести следующее наблюдение: если людоед $A$ сидит за столом №$i$, $i>1$, то он хочет съесть хотя бы кого-то за столом №$(i-1)$. В самом деле, он не хочет никого съесть за столами с номерами $\ge i$, иначе бы он был посажен за стол с номером строго больше $i$. Так как $i>1$, то он хочет съесть хоть кого-то. Однако если он не хочет никого съесть за столом №$(i-1)$, то мы бы посадили его за стол раньше. Наблюдение доказано. Из наблюдения следует, что, начиная с последнего посаженного людоеда, мы можем построить цепочку предпочтений длины равной количеству столов. По условию это число не превосходит $m$. Задача решена.

То же самое короче можно сказать так. Посадим людоеда $A$ за стол №$i$, если длиннейшая цепочка предпочтений $A \to \ldots$, начинающаяся с людоеда $A$, имеет длину $i$. Несложно проверить, что за столами конфликтов не возникает. $\square$

Чтобы сформулировать всё это чуть более наукообразно, введём терминологию частично упорядоченных множеств ¹. Будем говорить, что на множестве $S$ задан частичный порядок, если на некоторых (возможно, не всех) парах элементов из $S$ задано отношение сравнимости $\preceq$, удовлетворяющее свойствам:

транзитивность: если $a \preceq b$ и $b \preceq c$, то $a \preceq c$;
антисимметричность: $a \preceq b$ и $b \preceq a$ выполнены одновременно тогда и только тогда, когда $a=b$.

Строго говоря, частичный порядок – это просто подмножество декартова произведения $S \times S$, удовлетворяющее двум свойствам выше. Удобно думать, что мы объявляем некоторые пары элементов сравнимыми, отсюда и выбор обозначения $\preceq$. Простейшие примеры частично упорядоченных множеств: вещественные числа с отношением обычного сравнения $a \le b$; натуральные числа с отношением делимости $a | b$; подмножества некоторого фиксированного множества с отношением включения $a \subseteq b$. Для частично упорядоченного множества $(S,\preceq)$ будем писать $a \succeq b$, если $b \preceq a$; будем писать $a \prec b$, если $a \preceq b$ и $a\neq b$. Цепью называется множество элементов, которые можно упорядочить в виде последовательности $a_1 \prec \ldots \prec a_k$ ². Антицепью называется подмножество $B \subseteq S$, никакие два элемента которого не сравнимы друг с другом. В этой терминологии решение предыдущей задачи доказывает следующее утверждение³:

Теорема [Mirsky, 1971]. Если в конечном частично упорядоченном множестве максимальная цепь имеет мощность $m$, то всё множество можно накрыть $m$ антицепями.

Следствие. Если в конечном частично упорядоченном множестве максимальная цепь имеет мощность $m$, а максимальная антицепь имеет мощность $n$, то мощность всего множества не превосходит $mn$.

Следствие из следствия [Erdős–-Szekeres, 1935]. В последовательности из $mn + 1$ различных вещественных чисел можно найти либо возрастающую последовательность длины $m+1$, либо убывающую последовательность длины $n+1$.

Доказательство. Пусть нам дана последовательность $a_1, \ldots, a_{mn + 1}$ из попарно различных чисел. Введём искусственный частичный порядок на множестве $S = \{1,2,\ldots,mn+1\}$ так: будем писать $i \preceq j$, если $i \le j$ и $a_i \le a_j$. Цепи соответствуют возрастающим подпоследовательностям, антицепи – убывающим. Если все цепи имеют мощность не более $m$, а все антицепи имеют мощность не более $n$, то мощность $S$ не превосходит $mn$, что не так. $\square$

Теперь, когда мы прониклись теоремой Мирского, тем удивительней для нас будет обнаружить, что верен и двойственный результат, значительно более сложный.

Теорема [Dilworth, 1950]. Если в конечном частично упорядоченном множестве максимальная антицепь имеет мощность $n$, то всё множество можно накрыть $n$ цепями.

Доказательство теоремы Дилворта⁴ мы обсудим чуть ниже. Пока что давайте обратим внимание, что если $N$ – минимальное количество цепей, необходимое, чтобы покрыть всё множество $S$, то $n \le N$. В самом деле, ни одна цепь не может содержать двух элементов из максимальной (да и вообще ни из какой) антицепи. Теорема же утверждает, что $N \le n$. Поэтому на самом деле выполняется $N = n$, и для доказательства теоремы достаточно предъявить разбиение на цепи такое, что количество цепей разбиения равно размеру некоторой антицепи.

—1.6—

Одной из центральных идей первой части этого курса будет то, что вокруг леммы Холла есть целая плеяда теорем, в неформальном⁵ смысле эквивалентных лемме Холла. Теорема Дилворта – одна из них. Чтобы продемонстрировать эту связь, я приведу доказательство теоремы Дилворта, опирающееся на теорему Кёнига, которая, в свою очередь будет выведена из леммы Холла. Для начала вспомним терминологию двудольных графов. Пусть есть двудольный граф $G = (L \cup R, E)$ с долями $L$ и $R$ и множеством рёбер $E \subseteq L \times R$. Будем говорить, что вершина $v \in L \cup R$ покрывает ребро $e \in E$, если $v$ является одним из концов ребра $e$ (чаще в такой ситуации говорят, что ребро $e$ инцидентно вершине $v$). Подмножество вершин $U \subseteq L \cup R$ называется вершинным покрытием графа, если любое ребро покрыто какой-то вершиной из $U$.

Теорема [Kőnig, 1931]. В любом конечном двудольном графе размер максимального паросочетания равен размеру минимального вершинного покрытия.

Вывод теоремы Дилворта из теоремы Кёнига. Пусть нам дано конечно частично упорядоченное множество $(S,\preceq)$. Заведём двудольный граф $G$, обе доли которого являются копиями множества $S$: $L=S’, R=S’’$, где $S’, S’’$ – две изоморфные копии $S$. Для любой пары строго сравнимых элементов $a \prec b$ в $S$ нарисуем ребро между $a’ \in L$ и $b’’ \in R$. Здесь штрихами я обозначаю образы при соответствиях $S \overset{\cong}\to S’$, $S \overset{\cong}\to S’’$. Так мы определим множество рёбер $E$.

Применим теорему Кёнига. Пусть $M \subseteq E$ – максимальное паросочетание. Ясно, что любое вершинное покрытие, должно иметь размер не меньше $|P|$, так как у каждого ребра из $M$ хотя бы один из концов обязан входить в покрытие. Содержание теоремы Кёнига тогда такое: вершинное покрытие можно составить, выбирая ровно по одному концу у каждого ребра из $M$, и ничего кроме. Пусть $U$ это такое вершинное покрытие, $|U| = |M|$. Стартуя с $M$ и $U$, мы разобьём $S$ на цепи, так что количество цепей разбиения будет равно размеру некоторой антицепи. Этого достаточно для доказательства теоремы (в соответствии с тем, что было сказано в предыдущем параграфе).

Если ребро $(a’,b’’) \in M$, отнесём элементы $a,b \in S$ в одну цепь. Более общо, отнесём два элемента $a, b \in S$ в одну цепь, если они сравнимы через некоторую цепочку $a = a_1 < a_2 < \ldots < a_{k-1} < a_k = b$, такую что все соответствующие рёбра $(a_1’, a_2’’), \ldots, (a_{k-1}’, a_k’’)$ входят в $M$. Легко проверить, что так мы действительно получим разбиение на цепи, причём количество цепей будет равно $|S| - |M|$ ⁶. Осталось найти антицепь размера $|S| - |M|$. Для этого рассмотрим все элементы $a \in S$, такие что $a’ \in L \setminus U$ и $a’’ \in R \setminus U$. Их не менее $|S| - |U|$, и они образуют антицепь (по определению вершинного покрытия). Так как $|S| - |U| = |S| - |M|$, то мы нашли антицепь желаемого размера. $\square$

Вывод теоремы Кёнига из леммы Холла. Пусть $G = (L \cup R, E)$ – двудольный граф, и пусть $U = \underbrace{(U \cap L)}_{U_L} \cup \underbrace{(U \cap R)}_{U_R}$ – минимальное вершинное покрытие. Выше мы обсудили, что для доказательства теоремы достаточно привести пример паросочетания размера $|U|$. Другими словами, нам нужно найти паросочетание, в котором каждое ребро ровно одним концом задевает $U$. Эта идея – искать максимальное паросочетание – должна нам напомнить про графовую формулировку леммы Холла (—1.2—). Однако двудольный граф, для которого мы будем её применять, будет другим! Выбросим из рассмотрения множество $E_U$ всех рёбер, соединяющих $U_L$ и $U_R$ (потому что мы хотим избежать их использования в паросочетании). Все рёбра из $E \setminus E_U$ соединяют либо $U_L$ с $R\setminus U_R$, либо $U_R$ с $L\setminus U_L$ (здесь мы пользуемся тем, что $U$ – вершинное покрытие). Теперь рассмотрим двудольный граф с долями $U$ и $W = (L\cup R) \setminus U$ и рёбрами $E \setminus E_U$. Именно к нему мы применим лемму Холла, и построим паросочетание размера $|U|$.

Итак, нам нужно проверить посылки леммы Холла. Рассмотрим $k$-элементное подмножество $X \subseteq U$. Разобьём его на $X_L = X \cap U_L$ и $X_R = X \cap U_R$. Пусть $|X_L| = k_L$. Предположим, что “мальчики” из $X_L$ совокупно знакомы менее чем с $k_L$ “девочками” из $R\setminus U_R$. Тогда заменяя в множестве $U$ этих мальчиков из $X_L$ на их знакомых девочек, мы построим вершинное покрытие ⁷ исходного графа $G$ размера меньше, чем $U$. Это противоречит минимальности покрытия $U$. Значит, мальчики из $X_L$ совокупно знакомы хотя бы с $k_L$ девочками из $R\setminus U_R$. Аналогично, мальчики из $X_R$ совокупно знакомы хотя бы с $k_R = |X_R|$ девочками из $L\setminus U_L$. Следовательно, мальчики из $X$ совокупно знакомы хотя бы с $k = k_L + k_R$ девочками из $W$. Предположения леммы Холла верны, паросочетание размера $U$ существует. $\square$

—1.7—

Здесь мы обсудим простые оценки на мощность максимальной антицепи в $(S,\preceq)$ в одном важном случае: $S$ = подмножества некоторого фиксированного конечного множества, $\preceq$ = отношение включения $\subseteq$.

Теорема [Sperner, 1928]. Пусть $S$ – семейство некоторых подмножеств множества ${1,2,\ldots,n}$, причём никакие два подмножества из $S$ не вложены одно в другое. Тогда \[|S| \le {n \choose \lfloor n/2 \rfloor}.\]

Мы докажем эту теорему в чуть более общей формулировке ниже. Перед этим сделаем два замечания. Во-первых, оценка из теоремы Шпернера неулучшаема: достаточно положить в $S$ все подмножества размера $\lfloor n/2 \rfloor$. Во-вторых, давайте применим машинерию этой лекции к примеру с монотонными функциями из прошлой лекции (—1.3—). Тогда нам нужно было доказать, что булев куб $\{0,1\}^n$ можно разбить на ${n\choose \lfloor n/2 \rfloor}$ цепей. В самом деле, из теоремы Шпернера следует, что максимальная антицепь в булевом кубе имеет размер $\lfloor n/2 \rfloor$. Далее мы применяем теорему Дилворта и побеждаем.

Итак, вот обещанное обобщение теоремы Шпернера.

Теорема [Yamamoto, 1954; Meshalkin, 1963; Bollobás, 1965; Lubell, 1966]. Пусть $S$ – семейство некоторых подмножеств множества $\{1,2,\ldots,n\}$, причём никакие два подмножества из $S$ не вложены одно в другое. Пусть $s_k$ обозначает количество подмножеств размера $k$ в $S$. Тогда \[ \sum_{k=0}^{n} \frac{s_k}{ {n \choose k} } \le 1. \]

Так как ${n \choose k} \le {n\choose \lfloor n/2 \rfloor}$ для любого $k$, то теорема Шпернера следует из этого неравенства.

Доказательство. Каждому подмножеству $A \in S$ сопоставим следующие перестановки $\sigma$ чисел от одного до $n$, в которых вначале идут все числа из $A$ в каком-то произвольном порядке, а потом все числа не из $A$ в каком-то порядке. Тем самым каждому $A$ мы сопоставим ровно $|A|! (n - |A|)!$ перестановок. Более того, никакая перестановка не будет сопоставлена двум подножествам из $S$, иначе эти подмножества вложены одно в другое. Пересчитывая перестановки, сопоставленные хоть чему-то, получим \[ n! \ge \sum_{k=0}^n s_k \cdot k! (n - k)!, \] что эквивалентно требуемому. $\square$

В математическом сленге "частично упорядоченное множество" сокращают до "чум".
↩
В бесконечном случае цепью называется линейно упорядоченное подмножество, т.е. такое, что любые два его элемента сравнимы.
↩
Вообще говоря, в задаче про людоедов у нас не было транзитивности предпочтений, и в решении мы ей не пользовались. Тем не менее, требуя транзитивность в теореме Мирского, мы не умаляем её общности (подумайте, почему).
↩
Часто используют написание "Дилуорс".
↩
В том плане, что они красиво друг из друга выводятся.
↩
Можно думать об этом так: мы начинаем с разбиения на одноэлементные цепи, а рассмотрение каждого ребра из паросочетания объединяет какие-то две цепи в одну.
↩
Проверьте, что получилось действительно вершинное покрытие.
↩