Второй взгляд: лебегова размерность
—2.4—
Как и лемма Холла, лемма Шпернера – лишь одно из утверждений в большой серии “эквивалентных” теорем, которые для нас будут представлять интерес. Самое знаменитое из них – топологическая теорема Брауэра о неподвижной точке, мы доберёмся до неё чуть позже (как и до идеологии степени отображения, которая является для нас главным маяком). Начнём с несложных комбинаторных утверждений. Первое утверждение я буду называть коннектор-леммой 1 .
Лемма [Hochberg–McDiarmid–Saks, 1995]. Пусть вершины триангуляции \(n\)-мерного симплекса покрашены произвольно в цвета \(1, 2, \ldots, n\). Тогда можно выбрать какой-то цвет \(i\) так, что переходя только по рёбрам, соединяющим вершины цвета \(i\), можно от любой грани добраться до любой другой.
Доказательство. Предположим, не существует цвета, соединяющего все грани. Тогда для любой вершины триангуляции мы можем написать в ней метку, равную минимальному номеру грани, до которой нельзя дойти из данной вершины, шагая по вершинам одного цвета. Наши метки шпернеровские: на грани \(i\) нету меток \(i\). Найдём тогда радужный “разнометочный” симплекс. Метки в его вершинах различны, но цвета каких-то двух вершин совпадают (так как цветов всего \(n\)). Эти две вершины соединены ребром, имеют один цвет, но помечены разными метками. Это противоречит нашему алгоритму проставления меток. \(\square\)
Следующее утверждение я буду называть гекс-леммой, по названию игры гекс.
Лемма [Nash, 1948]. Рассматривается мелко триангулированный \(n\)-мерный куб \(I^n\). Каждому из \(n\) игроков назначены две противоположные гиперграни куба (суммарно покрывающие всю границу куба). Далее происходит следующая игра: игроки по очереди выставляют фишки своего цвета в вершины триангуляции (в каждой вершине может находиться лишь одна фишка). Выигрывает тот, кто первым сможет сможет соединить свои гиперграни цепочкой фишек своего цвета (в цепочке соседние вершины соединены рёбрами триангуляции). Утверждается, что такая игра не может закончиться ничьей.
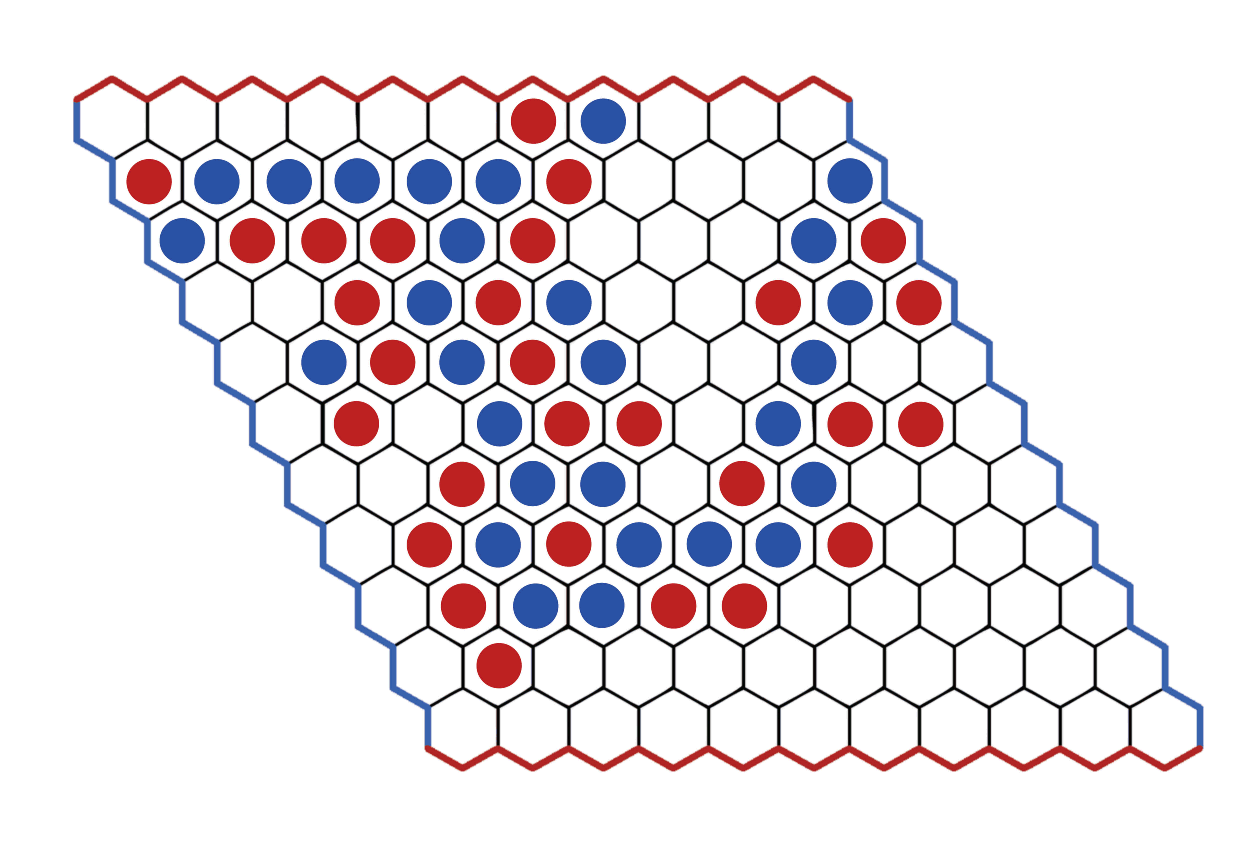
Доказательство. Предположим, все вершины заполнены фишками, но никто до сих пор не победил. Для каждого цвета \(i\) дорисуем одну новую вершину цвета \(i\) и соединим её со всеми вершинами одной из граней игрока \(i\). Несложно видеть, что на полученный граф можно можно смотреть как на триангуляцию симплекса. В этой триангуляции есть одноцветный коннектор цвета \(i\). Этот коннектор (с выброшенной новой вершиной, если в нём такая была) и даёт цепочку, гарантирующую победу игрока \(i\). \(\square\)
От гекс-леммы мы перейдём к её непрерывному аналогу, который иногда называют версией леммы Лебега, хотя доказал (в большей общности) её впервые Брауэр.
Лемма [continuous hex]. Если \(n\)-мерный единичный куб \(I^n\) покрыт \(n\) открытыми 2 множествами, то какие-то две противоположные грани можно соединить кривой, лежащей внутри одного из множеств.
Доказательство. Триангулируем куб очень мелко (чтобы каждое ребро триангуляции лежало целиком в одном из множеств покрытия), покрасим вершины в цвета, отвечающие накрывающим множествам (если вершина накрыта несколькими множествами, то можно выбрать любое из них), и применим дискретную гекс-лемму. \(\square\)
—2.5—
Другой непрерывный аналог леммы Шпернера – следующий результат Кнастера–Куратовского–Мазуркевича.
Лемма [Knaster–Kuratowski–Mazurkiewicz, 1929]. Если \(n\)-мерный симплекс \(\triangle^n\), гиперграни которого назовём \(F_0, \ldots, F_n\), покрыт открытыми (или замкнутыми) множествами \(U_0, \ldots, U_n\), так что \(F_i \cap U_i = \varnothing \forall i\), то \(\bigcap\limits_{i=0}^{n} U_i \neq \varnothing\).
Доказательство. Триангулируем симплекс очень мелко и покрасим вершины в цвета, отвечающие накрывающим множествам (если вершина накрыта несколькими множествами, то можно выбрать любое из них). Полученная раскраска – шпернеровская, поэтому найдётся разноцветный симплекс триангуляции. Если триангуляция была очень мелкая, то где-то внутри этого разноцветного симплекса мы хотели бы найти точку, принадлежащую всем множествам покрытия. Посмотрим на два способа оформить это заключение строго.
- Если все множества покрытия были замкнутыми, можно действовать в духе алгоритмов справедливого деления (—2.2—). Применим лемму Шпернера для серии всё более мелких триангуляций, найдём последовательность уменьшающихся разноцветных треугольников, и из соображений компактности найдём их предельную точку. Так как множества покрытия замкнуты, предельная точка им всем принадлежит.
- Если все множества покрытия были открытыми, мы можем применить стандартный аргумент, который легко найти в интернете по ключевой фразе “число Лебега”. Для любого открытого покрытия найдётся малое число \(\varepsilon > 0\), такое что любой шарик радиуса \(\varepsilon\) лежит целиком в одном из множеств покрытия. Выберем триангуляцию мелкости меньше \(\varepsilon\), тогда любая точка найденного разноцветного симплекса нам подойдёт. \(\square\)
—2.6—
Два непрерывных аналога леммы Шпернера, которые мы доказали в —2.4— и —2.5—, могут быть обобщены до так называемой леммы Лебега о покрытиях.
Лемма [Brouwer, 1913].
- Если \(n\)-мерный куб \(I^n\) покрыт конечным числом открытых (или замкнутых) множеств, никакое из которых не связывает две противоположные грани куба, то какая-то точка куба накрыта хотя бы \((n+1)\) множествами.
- Если \(n\)-мерный симплекс \(\triangle^n\) покрыт конечным числом открытых (или замкнутых) множеств, никакое из которых не связывает все грани симплекса, то какая-то точка симплекса накрыта хотя бы \((n+1)\) множествами.
Доказательство. Часть 1 следует из части 2 примерно из того же аргумента, из которого коннектор-лемма влечёт гекс-лемму. Детали я оставляю проверить читателю.
Чтобы доказать часть 2, для каждой компоненты связности каждого множества покрытия покрасим её в цвет \(i\), если эта компонента не задевает гипергрань симплекса с номером \(i\). По условию теоремы, такое \(i\) существует, а если таких \(i\) несколько, выберем любое. Пусть \(U_i\) – объединение всех компонент, покрашенных в цвет \(i\). Множества \(U_i\) удовлетворяют посылке леммы ККМ, из которой мы заключаем результат. \(\square\)
Смысл этой теоремы – топологическая инвариантность размерности. А именно, эта теорема нам говорит, как, обходясь только слабейшими внутренними топологическими свойствами пространства (но не пользуясь ни метрической структурой, ни структурой векторного пространства), можно определить понятие размерности. Впервые это понятие топологической размерности, или размерности в смысле покрытий, или размерности Лебега, явно определил Чех, а большие шаги на пути в этом и в смежных направлениях были сделаны Пуанкаре, Лебегом, Брауэром, Менгером и Урысоном.
Определение. Для нормального топологического пространства \(X\) размерностью Лебега называется наименьшее целое число \(n\) такое, что для всякого конечного открытого покрытия пространства \(X\) существует вписанное в него (конечное открытое) покрытие кратности \(n+1\).