Третий взгляд: степень отображения
—2.7—
В этой лекции я соберу несколько простых топологических следствий леммы Шпернера. Все эти утверждения объединены идеей степени отображения, дискретным суррогатом которой и является лемма Шпернера. Наш первый этюд – теорема о причёсывании ежа.
Теорема [Brouwer, 1912]. Не существует непрерывного ненулевого касательного поля к сфере \(S^2\).
Что значат эти слова? Мы считаем, что сфера \(S^2 = \{ (x,y,z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 \le 1 \}\) вложена в \(\mathbb{R}^3\) естественным образом. Касательным полем к сфере называется непрерывная вектор-функция \(v(\cdot)\), назначающая каждой точке \(x \in S^2\) касательный сфере вектор \(v(x)\). Теорема утверждает, что хотя бы один касательный вектор обязан обнулиться. Из популярных интерпретаций: на земном шаре не может повсюду быть ветер; морского ежа нельзя гладко причесать без проборов и завихрений.
Доказательство будет основано на следующей версии леммы Шпернера.
Лемма. Пусть многоугольник триангулирован, и каждая вершина триангуляции раскрашена в один из трёх цветов A, B, C. Обозначим через \(d_{AB}\) количество рёбер, покрашенных как AB, если мы обходим границу многоугольника по часовой стрелке; через \(d_{BA}\) – количество рёбер, покрашенных как BA при обходе по часовой стрелке. Тогда найдётся хотя бы \(|d_{AB} - d_{BA}|\) разноцветных треугольников.
Доказательство. Пусть, например, \(d_{AB} > d_{BA}\). Повторим доказательство с дверьми в замке (—2.1—). На этот раз ориентируем все двери AB так, что пройти в двери можно только в одном направлении (скажем, при проходе через дверь цвет A должен быть слева). Тогда в нашем замке \(d_{AB}\) внешних входов и \(d_{BA}\) выходов. Поэтому если мы будем гулять по замку, мы найдём как минимум \(d_{AB} - d_{BA}\) тупиковых (т.е. разноцветных) комнат. \(\square\)
Доказательство теоремы о причёсывании ежа. Предположим, ненулевое касательное поле \(v\) нашлось. Мы нарисуем на сфере ещё одно семейство ориентированных линий, которое будем называть координатными. Эти линии устроены так: это семейство окружностей, проходящих через северный полюс \(N\) и попарно друг друга касающихся. Получить представление о них можно из следующего рисунка, где мы выкололи малую окрестность южного полюса и растянули всё остальное на плоскости.
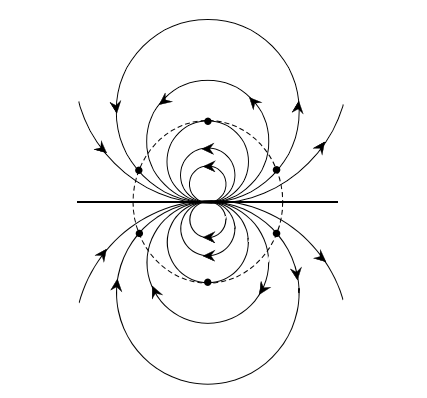
Это семейство линий, кстати, не противоречит теореме, так как не порождает касательного поля: возле северного полюса есть точки с касательными, смотрящими куда угодно.
Пусть \(\theta(x), x \neq N,\) – (ориентированный) угол между \(v(x)\) и направлением координатной линии в \(x\). Раскрасим точки сферы, кроме \(N\), в три цвета A, B, C в соответствии с тем, попадает ли \(\theta\) в диапазон \([0^\circ,120^\circ), [120^\circ,240^\circ), [240^\circ,360^\circ)\), соответственно. На рисунке пунктиром обозначена граница малой окрестности северного полюса. Под словом “малого” мы понимаем, что поле \(v\) на этой границе очень близко к значению в северном полюсе, и поэтому при обходе пунктирной границы на нашем рисунке вектор \(v\) совершает два полных оборота. Теперь триангулируем очень мелко всю сферу без окрестности северного полюса. Из сказанного следует, что \(|d_{AB} - d_{BA}| = 2\). Поэтому мы найдём разноцветный треугольник (даже два). Измельчая триангуляцию, и пользуясь соображениями компактности, найдём предельную точку разноцветных треугольников. В ней поле не может быть корректно определено, так как угол \(\theta\) должен одновременно лежать в \([0^\circ,120^\circ], [120^\circ,240^\circ], [240^\circ,360^\circ]\). \(\square\)
—2.8—
Пожалуй, наиболее известное применение леммы Шпернера – это вывод теоремы Брауэра о неподвижной точке.
Теорема [Bohl, 1904]. Любое непрерывное отображение \(f: B^n \to B^n\) \(n\)-мерного единичного шара в себя имеет неподвижную точку, т.е. точку \(x \in B^n\) такую, что \(f(x) = x\).
Доказательство. Теорему можно доказывать, заменив шар на любое гомеоморфное ему множество (осуществляя гомеоморфную “замену координат”). Будем доказывать утверждение для вероятностного симплекса \[ \triangle^n = \{ x = (x_0, x_1, \ldots, x_n) \in \mathbb{R}^{n+1} : x_0 \ge 0, \ldots, x_n \ge 0, \sum_i x_i = 1\}. \] Предположим, \(f(x) \neq x\) для всех \(x \in \triangle^n\). Тогда красим точку \(x\) в цвет \(i\), если \((f(x))_i < x_i\), и \(i\) – наименьший такой индекс, что это неравенство выполнено. Как обычно, мелко триангулируем наш симплекс, и замечаем, что раскраска получилась шпернеровская: грань, задаваемая \(x_i = 0\), не содержит цвета \(i\). Поэтому существует разноцветный треугольник, и как и раньше, мы можем найти предельную точку \(\hat x\) разноцветных треугольников в последовательности измельчающихся триангуляций. Эта точка должна быть неподвижной, так как \((f(\hat x))_i \le \hat x_i\) для всех \(i\). \(\square\)
—2.9—
В качестве одного занятного приложения теоремы Брауэра мы взглянем на один этюд по мотивам известной теоремы Жордана о том, что что несамопересекающаяся кривая на плоскости разбивает её на две связные части. Часто про эту теорему думают как про неприятную, однако её не так уж сложно вывести из теоремы Брауэра 1 . Мы ограничимся одним важным частным случаем.
Теорема. Пусть в прямоугольнике на плоскости нарисованы две кривые \(\gamma_1, \gamma_2: [-1,1] \to [a,b]\times [c,d]\), причём \(\gamma_1\) соединяет левую сторону прямоугольника с правой, а \(\gamma_2\) соединяет верхнюю сторону с нижней. Тогда кривые пересекаются.
Доказательство. Пусть кривые заданы координатно как \(\gamma_1(t) = (x_1(t), y_1(t))\), \(\gamma_2(t) = (x_2(t), y_2(t))\). Если предположить, что кривые не пересекаются, то корректно определено отображение \[ A(s,t) = \frac{(-x_1(s)+x_2(t), y_1(s) -y_2(t) )}{\max (|x(s)-x_2(t)|, |y_1(s) -y_2(t)|)} \] квадрата \([-1,1] \times [-1,1]\) в себя. Мы проверим, что у него нет неподвижных точек, и это будет противоречить теореме Брауэра. Из формулы ясно, что образ \(A\) лежит на границе квадрата. Значит, неподвижная точка обязана быть на границе. При этом левая сторона квадрата \(s=-1\) отображается в правую полуплоскость, так как \(-x_1(s)+x_2(t) = -a + x_2(t) \ge 0\). Аналогично, остальные стороны квадрата тоже не могут иметь неподвижную точку. \(\square\)
-
Доказательство опубликовано Ryuji Maehara.
↩