Первый взгляд на лемму Шпернера

—1—

Первый сюжет, который я хочу осветить, начинается с “олимпиадной” комбинаторной леммы. Первая важная идея этого курса такая: дискретные идеи, с которыми мы познакомимся, несложно превратить в непрерывные, и это приведёт нас к элементарным доказательствам некоторых топологических теорем. На этом пути мы познакомимся с несколькими ранними триумфами топологии, объединёнными вокруг понятия топологической размерности.

Лемма. Пусть на плоскости нарисован треугольник \(\triangle\) с вершинами \(v_0, v_1, v_2\). Пусть дана триангуляция \(\triangle\), т.е. разбиение \(\triangle\) на меньшие треугольники, так что любые два треугольника разбиения пересекаются либо по общему ребру, либо по общей вершине, либо не пересекаются вообще. Пусть также вершины триангуляции покрашены в цвета 0, 1, 2, так что сторона \(v_0 v_1\) не содержит цвета 2, сторона \(v_0 v_2\) не содержит цвета 1, сторона \(v_1 v_2\) не содержит цвета 0. Тогда найдётся разноцветный (или радужный) треугольник триангуляции, т.е. треугольник разбиения, все вершины которого покрашены в разные цвета.

Доказательство 1. Посмотрим на триангуляцию как на план замка, в которой треугольники триангуляции обозначают комнаты, рёбра типов 0-2 и 1-2 обозначают стены, а рёбра типа 0-1 обозначают двери. Нарисуем двойственный граф \(G\), вершинами которого являются комнаты (а также внешность замка), а рёбра которого соответствуют дверям между комнатами.

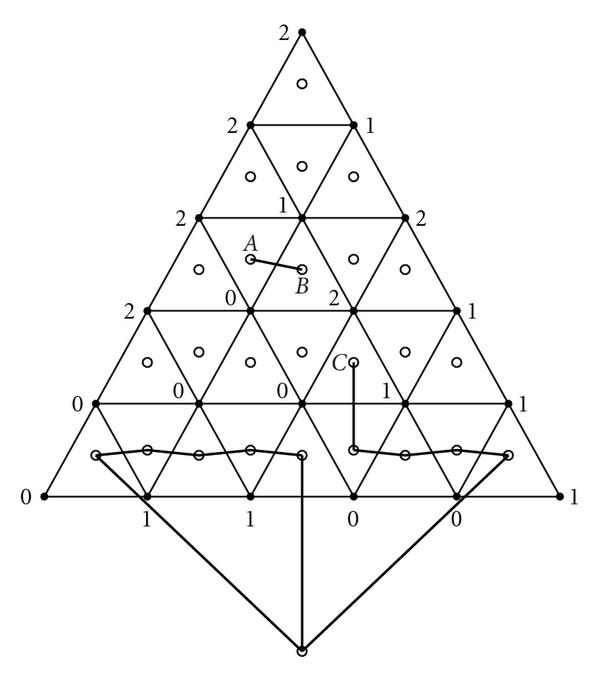
Проследим за степенями вершин в графе \(G\). Внутренние комнаты, не являющиеся разноцветными, имеют степень 0 или 2. Разноцветные комнаты, если они есть, имеют степень 1. Внешняя комната имеет степень, равную числу “переключений” 0-1 и 1-0 про проходе вдоль стороны \(v_0v_1\). Это число нечётное. В любом графе количество вершин нечётной степени чётно (доказательство: подсчёт числа рёбер по степеням вершин). Поэтому кроме внешней комнаты, есть ещё нечётное число внутренних комнат нечётной степени, т.е. разноцветных. Поэтому такая комната существует хотя бы одна. \(\square\)

Доказательство 2. Пусть наш рисунок нарисован в декартовой плоскости \(xOy\). Запустим следующий динамический процесс: пусть каждая вершина \(u\) триангуляции цвета \(i\) линейно движется из своего стартового положения в конечное положение \(v_i\). Движение будет запараметризовано временем \(t\in[0,1]\), т.е. мы имеем движущуюся вершину \(u(t) = (1-t) u + t v_i\). Мы будем следить за непрерывной деформацией триангуляции. В конечный момент времени \(t=1\) триангуляция станет вырожденной: все вершины триангуляции окажутся в вершинах \(\triangle\). Что происходит с каждым отдельным треугольником \(\triangle_i\) триангуляции? Неразноцветные треугольники вырождаются — схлопываются в отрезок или точку. Разноцветные треугольники растягиваются, чтобы совпасть с \(\triangle\). Что происходит с ориентированной площадью \(S_i(t)\) треугольника \(\triangle_i\)? Это квадратичная функция \(t\) (так как может быть выписана в виде подходящего детерминанта, состоящего из линейных функций переменной \(t\)). Ориентацию площади мы выбираем так, чтобы в начальный момент все площади \(S_i(0)\) были положительны. В процессе движения площадь \(S_i(t)\) может поменять знак, если треугольник проходит через вырожденное положение и меняет ориентацию. Тем не менее, можно считать, что на малом промежутке времени \([0,\varepsilon)\) все площади \(S_i(t)\) положительны. Шпернеровское условие (\(v_iv_j\) не содержит цвета \(k\), где все \(i,j,k\) различны) означает, что на малом промежутке времени \([0,\varepsilon)\) деформированная картинка всё ещё является триангуляцией \(\triangle\). Тем самым, полиномиальная функция \[ \sum_{i} S_i(t) \] является константой на полуинтервале \([0,\varepsilon)\), а значит она константа на отрезке \([0,1]\). Значит, \[ \sum_{i} S_i(1) = S_{\triangle}. \] Ненулевые слагаемые слева (которые могут быть равны только \(\pm S_{\triangle}\)) отвечают разноцветным треугольникам, и поэтому их количество нечётно. \(\square\)

Лемма Шпернера [Sperner, 1928]. Пусть \(d\)-мерный симплекс \(\triangle\) с вершинами \(v_0, v_1, \ldots, v_d\) триангулирован, и вершины триангуляции покрашены в цвета \(0,1, \ldots, d\), так что гипергрань¹ \(v_0 \ldots \widehat{v_i} \ldots v_d\) не содержит цвета \(i\), \(0 \le i \le d\). Тогда количество разноцветных симплексов триангуляции нечётно.

Доказательство. Можно получить индуктивное доказательство, следуя идее доказательства 1 выше. При этом для подсчёта степени внешней вершины двойственного графа воспользоваться утверждением леммы Шпернера на единичку меньшей размерности. Можно получить и прямое рассуждение, повторяя идею доказательства 2 выше. Нужно использовать, что объёмы симплексов триангуляции могут быть выписаны как многочлены (детерминанты) от координат. \(\square\)

—2—

Одно из неожиданных применений леммы Шпернера — справедливое деление. Знаменитый пример, предложенный Фрэнсисом Су: пусть нам нужно поделить пирог на троих капризных людей \(A,B,C\)². Пирог будет замоделирован отрезком \([0,1]\) (если не устраивает такая модель пирога, пусть это будет колбаса). У каждого из людей свои особые предпочтения насчёт разных участков пирога, и мы их не знаем. Всё что мы можем узнать от этих людей, формулируется так.

• Для любого деления пирога на три части (задаваемой двумя координатами разреза \(0\le x \le y \le 1\)) мы можем спросить любого человека, какую часть из трёх тот находит наиболее предпочтительной. Вообще говоря, человеку может быть безразлично, какой из двух или из трёх кусков выбрать, т.е. предпочтения могут быть многозначными; в этом случае человек может при ответе на вопрос указать любой из предпочитаемых кусков.
• Никто не выберет пустой кусок.
• Предпочтения замкнуты в следующем смысле: если для разрезаний \(0\le x_i \le y_i \le 1\)), где последовательности \(x_i, y_i\) сходящиеся, некий человек всегда предпочитает кусок \(k\), то и для предельного разрезания \(0\le \lim x_i \le \lim y_i \le 1\)) этот человек не будет возражать против куска \(k\).

Заметим, что пространство всех делений пирога \[ \triangle = \{(x,y) \in \mathbb{R}^2 : 0\le x \le y \le 1\} \] есть треугольник. Его вершины суть \(v_0 = (0,0), v_1 = (0,1), v_2 = (1,1)\). Разделим его на маленькие треугольнички регулярным образом (линиями, параллельными сторонам). Каждая вершина разбиения будет назначена одному из участников, как на картинке:

Вершины помечены таким образом, чтобы у любого треугольника нашей специальной триангуляции вершины были помечены разными людьми.

Для каждой вершины разбиения \((x,y)\) зададим вопрос соответствующему участнику деления: “какой кусок пирога при этом делении предпочли бы вы?”. Ответ \([0,x]\) кодируем числом (цветом) 2, ответ \([x,y]\) — цветом 1, ответ \([y,1]\) — цветом 0. Если ответ неоднозначен, мы красим вершину в любой из соответствующих цветов. Таким образом мы получаем раскраску вершин триангуляции. Проверим шпернеровское условие. Сторона \(v_0v_1\) (отвечающая \(x=0\)) не содержит цвета 2 — это дано нам условием “никто не выберет пустой кусок”. Аналогично с двумя другими сторонами. Значит выполнено заключение леммы Шпернера, и найдётся разноцветный треугольник. Если полагать, что наша триангуляция была настолько мелкой, что участники не переживают из-за вариации величины пирога такого порядка, то мы победили. Действительно, на вопросы о желанном куске для трёх близких параметров разрезания три человека дали три разных ответа, поэтому любое такое разрезание удовлетворит всех троих. Если же мы хотим точный ответ, что мы можем подразбить \(\triangle\) на ещё более мелкие треугольники (таким же регулярным образом), и повторить процедуру, найдя более мелкий разноцветный треугольник. Повторяем эту процедуру для мелкости разбиения, стремящейся к нулю, и из соображений компактности находим предельную точку найденных разноцветных треугольников. В соответствии с предположением о замкнутости предпочтений предельная точка даст нам оптимальное разрезание пирога.

Другое применение лемме Шпернера нашлось в вопросе справедливого деления арендной платы. Пусть у нас есть три друга \(A,B,C\), которые собрались снимать жильё суммарной арендной платы 1 у.е. в месяц. В квартире три комнаты, у и трёх участников дележа разные предпочтения насчёт того, насколько эти комнаты хороши. Правила таковы.

• Для любого разделения аренды на три части, соответствующие трём комнатам (разделение задаваётся числами \(0\le x \le y \le 1\)), мы можем спросить любого человека, какую комнату из трёх тот находит наиболее предпочтительной при заданной плате. Опять-таки, предпочтения могут быть многозначными.
• Любой человек согласится на бесплатную комнату.
• Предпочтения замкнуты в следующем смысле: если для разделений аренды \(0\le x_i \le y_i \le 1\)), где последовательности \(x_i, y_i\) сходящиеся, некий человек всегда предпочитает комнату \(k\), то и для предельного разделения \(0\le \lim x_i \le \lim y_i \le 1\)) этот человек не будет возражать против комнаты \(k\).

Аналогичная предыдущему рассуждению с пирогом процедура приводит к алгоритму, в котором есть один нюанс. Раскраска триангуляции оказывается не шпернеровская, а наоборот: относительная внутренность стороны \(v_0v_1\) (отвечающей \(x=0\)) содержит только цвет 2, и так далее. Нам нужен тогда соответствующий (если угодно, двойственный) вариант леммы Шпернера, утверждающий, что в такой раскраске всё равно найдётся разноцветный треугольник. Эта версия леммы Шпернера действительно верна, и может быть сравнительно просто выведена из обычной леммы Шпернера. Я оставлю детали этого рассуждения читателю, но подскажу, что наш треугольник можно погрузить как серединный внутрь вдвое большего треугольника, и на большем треугольнике доопределить раскраску, чтобы она была шпернеровской.

Многомерные аналоги алгоритмов справедливого деления строятся таким же образом. Один из нюансов состоит в том, как выбирать “регулярную” триангуляцию, которую удастся пометить участниками дележа. Ответ может быть такой: имея любую мелкую триангуляцию симплекса, можно рассмотреть её барицентрическое подразбиение, которое уже несложно пометить правильным образом.

—Cсылки—

• E. Sperner, Neuer Beweis für die Invarianz der Dimensionszahl und des Gebietes. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (1928).
• F.E. Su, Rental harmony: Sperner’s lemma in fair division. The American mathematical monthly (1999).
• Статья в The New York Times про арендную гармонию со смешным апплетом.
• Видео Mathologer’а с одним из доказательств в 2D и применением к арендной гармонии.