Пятый взгляд: причёсывание ежа

—10—

В этой лекции я соберу несколько простых топологических следствий леммы Шпернера. Все эти утверждения объединены идеей степени отображения, дискретным суррогатом которой и является лемма Шпернера. Наш первый этюд — теорема о причёсывании ежа.

Теорема [Poincaré, 1885]. Не существует непрерывного ненулевого касательного поля к сфере \(S^2\).

Что значат эти слова? Мы считаем, что сфера \(S^2 = \{ (x,y,z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 \le 1 \}\) вложена в \(\mathbb{R}^3\) естественным образом. Касательным полем к сфере называется непрерывная вектор-функция \(v(\cdot)\), назначающая каждой точке \(x \in S^2\) касательный сфере вектор \(v(x)\). Теорема утверждает, что хотя бы один касательный вектор обязан обнулиться. Из популярных интерпретаций: на земном шаре не может повсюду быть ветер; морского ежа нельзя гладко причесать без проборов и завихрений.

Доказательство будет основано на следующей версии леммы Шпернера.

Лемма. Пусть многоугольник триангулирован, и каждая вершина триангуляции раскрашена в один из трёх цветов A, B, C. Обозначим через \(d_{AB}\) количество рёбер, покрашенных как AB, если мы обходим границу многоугольника по часовой стрелке; через \(d_{BA}\) — количество рёбер, покрашенных как BA при обходе по часовой стрелке. Тогда найдётся хотя бы \(|d_{AB} - d_{BA}|\) разноцветных треугольников.

Доказательство. Пусть, например, \(d_{AB} > d_{BA}\). Повторим доказательство с дверьми в замке (—1—). На этот раз ориентируем все двери AB так, что пройти в двери можно только в одном направлении (скажем, при проходе через дверь цвет A должен быть слева). Тогда в нашем замке \(d_{AB}\) внешних входов и \(d_{BA}\) выходов. Поэтому если мы будем гулять по замку, мы найдём как минимум \(d_{AB} - d_{BA}\) тупиковых (т.е. разноцветных) комнат. \(\square\)

Доказательство теоремы о причёсывании ежа. Предположим, ненулевое касательное поле \(v\) нашлось. Мы нарисуем на сфере ещё одно семейство ориентированных линий, которое будем называть координатными. Эти линии устроены так: это семейство окружностей, проходящих через северный полюс \(N\) и попарно друг друга касающихся. Получить представление о них можно из следующего рисунка, где мы выкололи малую окрестность южного полюса и растянули всё остальное на плоскости.

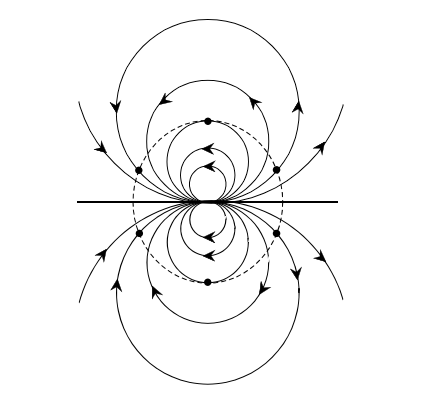
Это семейство линий, кстати, не противоречит теореме, так как не порождает касательного поля: возле северного полюса есть точки с касательными, смотрящими куда угодно.

Пусть \(\theta(x), x \neq N,\) — (ориентированный) угол между \(v(x)\) и направлением координатной линии в \(x\). Раскрасим точки сферы, кроме \(N\), в три цвета A, B, C в соответствии с тем, попадает ли \(\theta\) в диапазон \([0^\circ,120^\circ), [120^\circ,240^\circ), [240^\circ,360^\circ)\), соответственно. На рисунке пунктиром обозначена граница малой окрестности северного полюса. Под словом “малого” мы понимаем, что поле \(v\) на этой границе очень близко к значению в северном полюсе, и поэтому при обходе пунктирной границы на нашем рисунке вектор \(v\) совершает два полных оборота. Теперь триангулируем очень мелко всю сферу без окрестности северного полюса. Из сказанного следует, что \(|d_{AB} - d_{BA}| = 2\). Поэтому мы найдём разноцветный треугольник (даже два). Измельчая триангуляцию, и пользуясь соображениями компактности, найдём предельную точку разноцветных треугольников. В ней поле не может быть корректно определено, так как угол \(\theta\) должен одновременно лежать в \([0^\circ,120^\circ], [120^\circ,240^\circ], [240^\circ,360^\circ]\). \(\square\)

—11—

Половина предыдущих сюжетов в одно предложение объясняется идеей степени отображения, замечательной топологической концепцией, придуманной Брауэром. Пришло время её ввести.

Для начала мы определим, что называется степенью кусочно-линейного отображения сфер.

Триангуляцией¹ сферы \(S^n\) будем называть отождествление сферы с границей выпуклого \((n+1)\)-мерного многогранника, все грани которого являются симплексами. Таким образом, сфера обретает структуру симплициального комплекса (что бы это ни значило), от которой мы будем использовать следующие свойства.

• Сфера представляет собой объединение \(n\)-мерных симплексов, которые пересекаются только по граничным точкам.
• Помимо \(n\)-симплексов, частью симплициальной структуры являются всевозможные их грани, \(k\)-симплексы при \(0 \le k \le n\).
• Любые два симплекса либо не пересекаются вообще, либо пересекаются по общей грани, тоже симплексу.
• Каждый из \(n\)-симплексов гомеоморфен стандартному симплексу \(\{(x_0, \ldots, x_n) \in \mathbb{R}^{n+1} ~\vert~ x_i \ge 0, \sum x_i = 1\}\), а потому в каждом симплексе сферы имеют смысл «барицентрические координаты», и любая точка сферы может быть представлена в этом смысле как выпуклая комбинация \(\le n+1\) вершин одного из симплексов.
• Триангуляция связна в следующем смысле: между любыми двумя \(n\)-симплексами можно перейти по цепочке \(n\)-симплексов, в которой любые два соседних симплекса пересекаются по \((n-1)\)-симплексу.

Ориентацией симплекса \(\triangle^n\) называется выбор одного из двух классов упорядочивания его вершин; для любых двух нумераций вершин числами от \(0\) до \(n\) можно рассмотреть перестановку \(\sigma \in S_{n+1}\), переводящую одну в другую, и если она чётная, то класс один, а если нечётная, то классы разные. Ориентация на симплексе \(\triangle^n\) индуцирует ориентацию на любой его \((n-1)\)-мерной грани. Два \(n\)-симплекса, смежных по \((n-1)\)-грани, ориентированы согласованно, если они индуцируют противоположные ориентации на общей \((n-1)\)-грани.

Утверждение. Любая триангуляция сферы \(S^n\) может быть ориентирована согласованным образом. Кажется, проще всего это понять, если дополнить триангуляцию сферы до триангуляции шара \(B^{n+1}\), добавляя новую вершину в центр сферы и соединяя её со всем, что на сфере происходит. Триангуляция шара может быть наделена (самосогласованной) ориентацией просто из свойств объемлющего пространства \(\mathbb{R}^{n+1}\). А именно, у любого \((n+1)\)-симплекса вершины можно пронумеровать \(v_0, \ldots, v_{n+1}\) так, чтобы базис \(v_1-v_0, \ldots, v_{n+1} - v_0\) был ориентирован так же, как и стандартный базис \(\mathbb{R}^{n+1}\) (то есть чтобы матрица перехода от одного к другому имела положительный детерминант).

Отображение \(f: S^n \to S^n\) называется кусочно-линейным, если существуют такие триангуляции сферы-прообраза и сферы-образа, что отображение \(f\) переводит \(k\)-симплексы первой в \((\le k)\)-симплексы второй (в частности, вершины в вершины), и при этом в ограничении на любой симплекс это отображение линейно (в смысле локальных барицентрических координат). Другими словами, если точка в сфере-прообразе представляется как выпуклая комбинация \(x = \sum \lambda_i v_i\) (где \(v_i\) — вершины одного симплекса), то во-первых, \(f(v_i)\) — вершины одного симплекса в образе (возможно, с повторениями), и во-вторых, \(f(x) = \sum \lambda_i f(v_i)\).

Определение. Степенью кусочно-линейного отображения \(f: S^n \to S^n\) между ориентированными триангулированными сферами называется число \[ \deg f = \sum_{x \in f^{-1}(y)} \text{sign } df_x, \] где

• \(y\) — любая точка во внутренности любого \(n\)-симплекса в образе,
• число \(\text{sign } df_x\) положено равным \(+1\), если \(f\) сохраняет ориентацию \(n\)-симплекса, содержащего точку \(x\), и \(-1\), если не сохраняет.

Чтобы проверить корректность этого определения, нужно показать, что оно не зависит от точки \(y\) в образе. Достаточно проверить это для двух точек \(y\) и \(y’\), содержащихся в соседних симплексах \(\triangle\) и \(\triangle’\). Я приведу здесь картинку, из которой легко себя в этом убедить: грани, висящие над \(\triangle \cap \triangle’\), смежны чётному количеству \(n\)-симплексов, висящих над \(\triangle\) и \(\triangle’\), и эти \(n\)-симплексы привносят одинаковый суммарный вклад в степени, посчитанные над точками \(y\) и \(y’\).

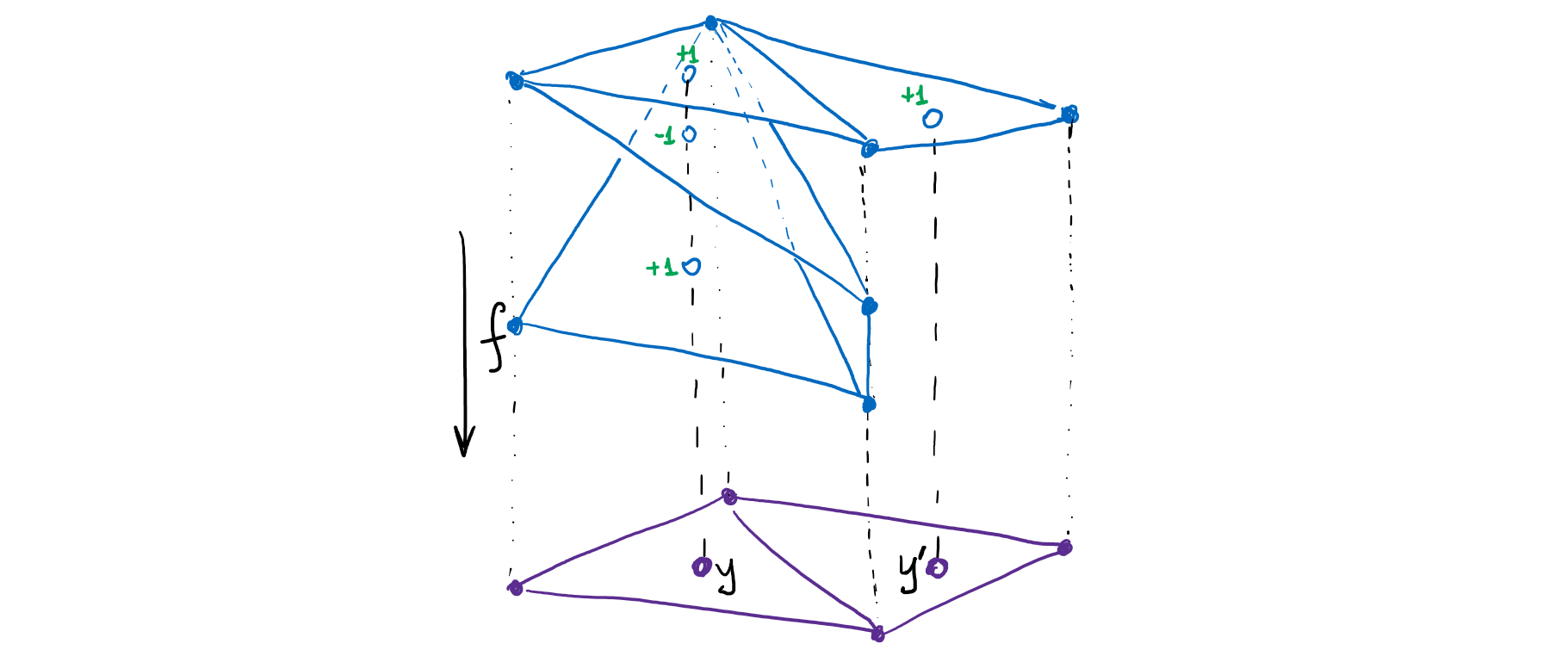
Как определение степени упрощает жизнь, мы увидим далее. Неформальный его смысл — это «сколько раз одна сфера оборачивается вокруг другой», или «сколько прообразов, посчитанных алгебраически (со знаками), у общей точки в пространстве образов». Пока же я оставлю здесь комментарий по поводу общности моего определения.

• Хоть я и рассматривал здесь случай отображений сфер, можно определить степень для отображений ориентированных многообразий одной размерности (возможно, с границами). Для неориентируемых многообразий можно определить степень по модулю два.
• Для гладких отображений степень традиционно определяется примерно так же (число прообразов у общей точки, посчитанное со знаками, происходящими из знака якобиана).
• Для непрерывных отображений степень чаще всего определяется через индуцированное отображение в гомологиях пространств, но можно и просто приблизить непрерывное отображение гладким или кусочно-непрерывным, и воспользоваться определением через алгебраическое число прообразов.

—Ссылки—

• H. Poincaré, Sur les courbes définies par les équations différentielles. Journal de Mathématiques Pures et Appliquées (1885).
• Лучшее изложение степени с дифференциальной точки зрения можно прочитать в замечательной книге Милнора.