Шестой взгляд: степень отображения

—12—

Я хочу объяснить два главных свойства степени отображения.

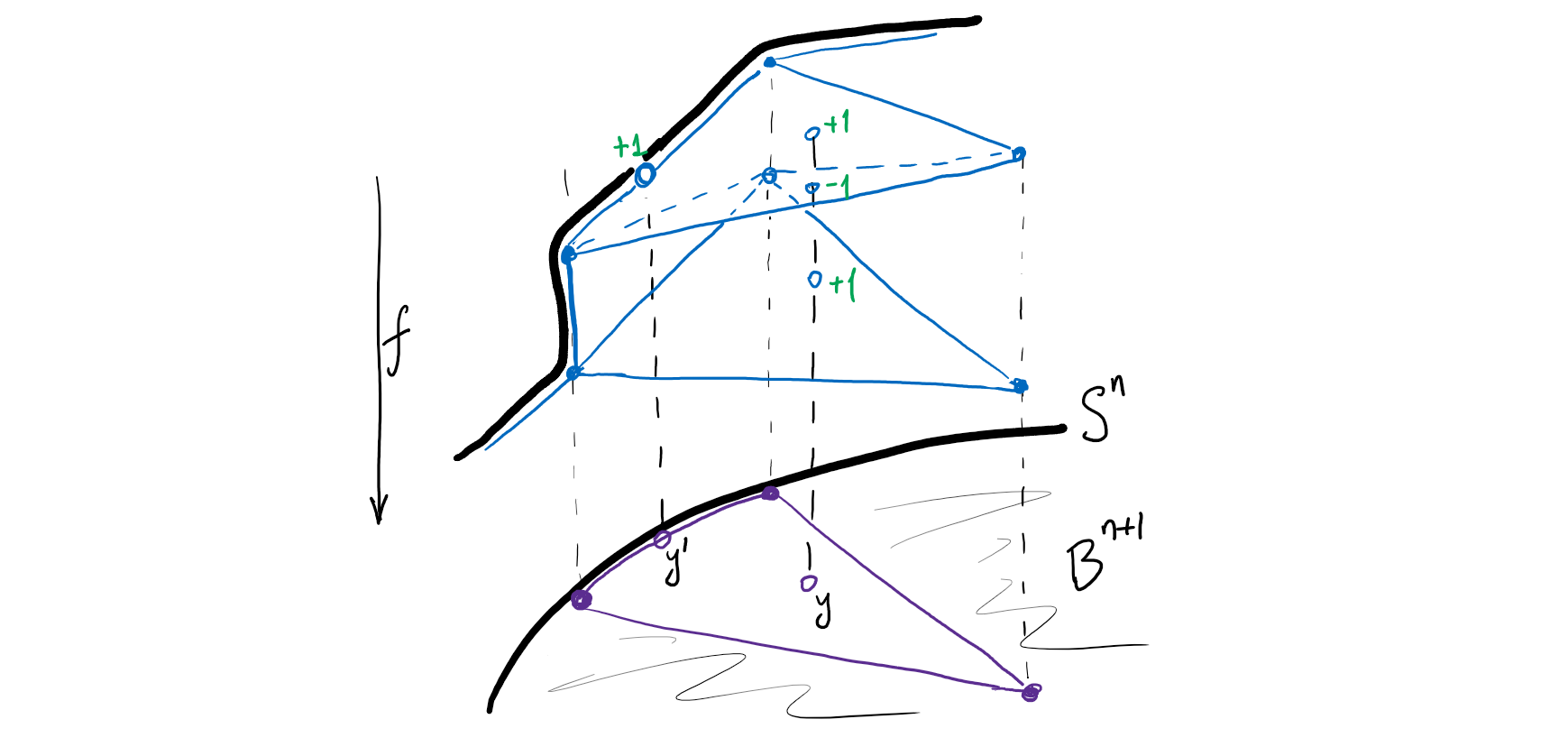
Представим, что кусочно-линейное отображение \(f : S^n \to S^n\) продолжается до кусочно-линейного отображения \(\bar f : B^{n+1} \to B^{n+1}\). Про оба шара можно думать как про \((n+1)\)-мерные триангулированные многогранники, отображение между которыми кусочно-линейно в смысле —11—. Удобно также считать, что ориентация этих триангуляций унаследована из объемлющего пространства \(\mathbb{R}^{n+1}\). Степень такого отображения можно определелить, как и раньше: \[ \deg \bar f = \sum_{x \in \bar f^{-1}(y)} \text{sign } d\bar f_x, \] где \(y\) — любая точка во внутренности любого старшего симплекса в образе. Проверка корректности этого определения, которую я оставляю читателю, использует тот факт, что \(\bar f\) отправляет границу шара в границу. В таких случаях говорят, что \(\bar f\) — отображение пар \((B^{n+1}, S^n) \to (B^{n+1}, S^n)\).

Степень отображения пар (шар, граничная сфера)¹ равно степени отображения границ: \[\deg f = \deg \bar f.\]

Объяснение этому следует из вглядывания в ту же самую картинку, что и для корректности определения степени:

Другое важнейшее наблюдение состоит в том, что если отображение непрерывно «деформировать», то его степень не изменится. Я определю это в комбинаторном сеттинге для случая сфер.

Говорят, что кусочно-линейные отображения \(f_0, f_1 : S^n \to S^n\) гомотопны, если существует кусочно-линейное² отображение \(F: S^n \times [0,1] \to S^n\), которое на краях «цилиндра» ограничивается в \(f_0\) и \(f_1\). Это означает, что \(F(x, 0) = f_0(x)\) и \(F(x, 1) = f_1(x)\). Обозначение: \(f_0 \sim f_1\). Про гомотопию \(F\) удобно думать как про параметрическое семейство отображений \(F(\cdot, t) = f_t(\cdot) : S^n \to S^n\), интерполирующее между \(f_0\) и \(f_1\).

Степень отображения — гомотопический инвариант³; если \(f_0 \sim f_1\), то \[\deg f_0 = \deg f_1.\]

Убедить себя в этом можно из следующего рисунка:

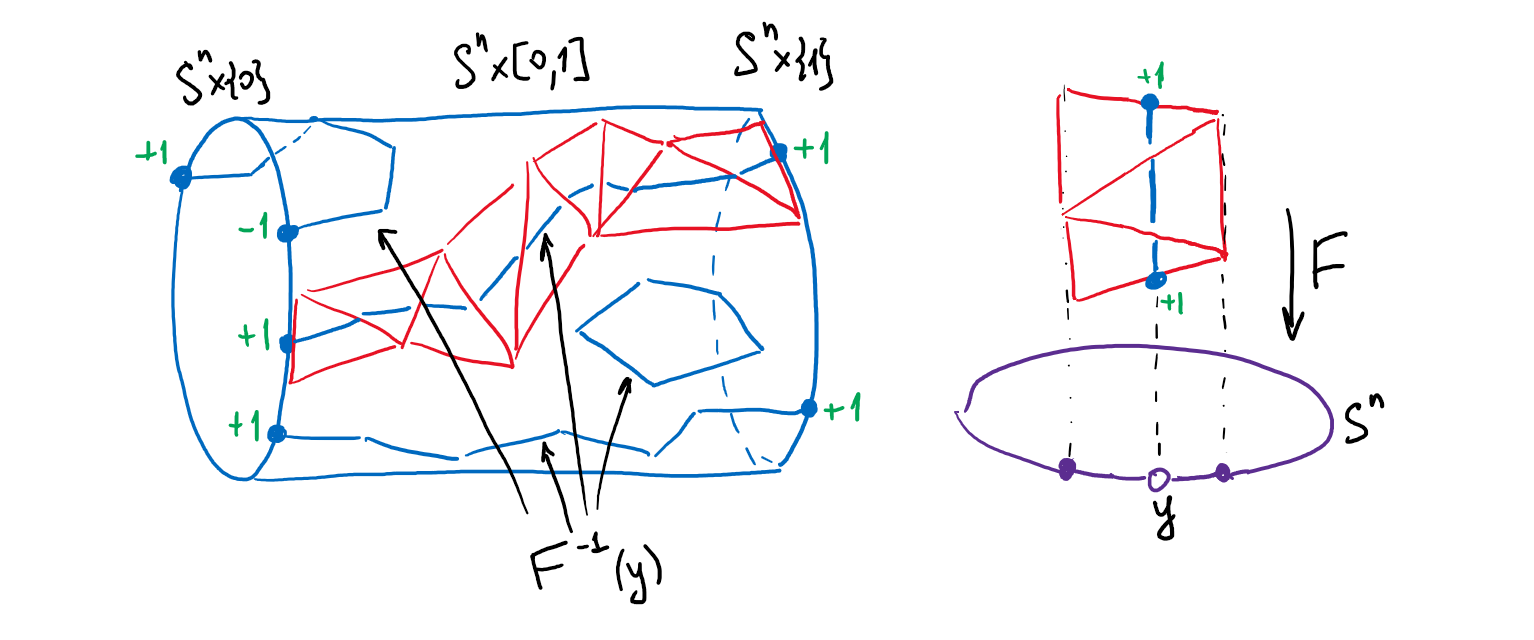
Если \(y \in S^n\) — точка в образе, находящаяся внутри старшего симплекса триангуляции, относительно которой \(F\) симплициально, то прообраз \(F^{-1}(y)\) представляет собой семейство кривых в цилиндре, каждая из которых

• либо соединяет два края цилиндра, \(S^n\times\{0\}\) и \(S^n\times\{1\}\), и вносит одинаковый вклад в степени \(\deg f_0\) и \(\deg f_1\),
• либо соединяет две точки на одном краю, и вклады этих двух точек в соответствующую степень взаимно уничтожаются,
• либо замкнутая петля, не выходящая на края. Вопрос согласования знаков нужно проверить; это следует из того, что если \((n+1)\)-симплекс цилиндра отображается на \(n\)-симплекс \(\triangle \subset S^n\), ровно две его \(n\)-грани накрывают \(\triangle\), причём с разной ориентацией.

Два свойства — ограничение степени на границу и гомотопическая инвариантность — интересно сравнить с двумя доказательствами леммы Шпернера (—1—). Шпернеровская раскраска симплекса задаёт кусочно-линейное отображение симплекса в себя, сохраняющее каждую грань. Два доказательства того, что степень этого отображения нечётна, мимикрируют два рассмотренных свойства степени. Лемма шпернеровского типа из —10— в свете свойств степени также становится почти очевидной.

—13—

Хайнц Хопф полностью классифицировал гомотопические классы отображений сферы в себя.

Теорема [Hopf, 1927]. Отображения \(f_0, f_1 : S^n \to S^n\) гомотопны тогда и только тогда, когда их степени равны.

На современном языке гомотопических групп это означает, что \(\pi_n(S^n) = \mathbb{Z}\). Вопрос о старших гомотопических группах \(\pi_m(S^n), m > n\), во многом определил развитие алгебраической топологии на много лет вперёд, и есть все основания считать, что мы никогда не узнаем, чему равна \(\pi_{100}(S^2)\).

Набросок доказательства методом оснащённых кобордизмов Понтрягина.

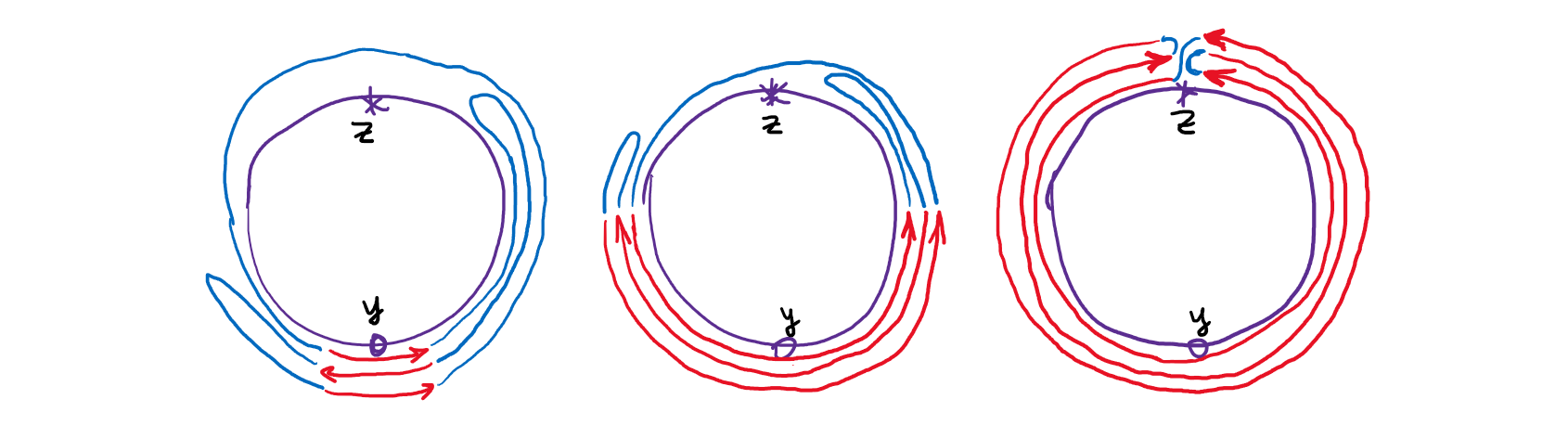
Первый шаг: приведение произвольного отображения \(f: S^n \to S^n\) к некому модельному «понтрягинскому» виду. Выбираем точку \(y\) в образе (во внутренности любого старшего симплекса). Пусть \(V\) — её малая открестность⁴. Далее «включаем» гомотопию, которая растягивает \(V\) на всю сферу (так что края \(V\) в итоге замкнутся в точке \(z \in S^n\), противоположной к \(y\)). При этой гомотопии каждая точка вне \(V\) может просто ехать в сторону \(z\) по геодезической с постоянной скоростью. В конце этого процесса отображение \(f\) превращается в модельное \(f’\), устроенное следующим образом: в сфере-прообразе выбрано конечное число непересекающихся дисков, каждый из которых оборачивается вокруг сферы-образа одним из двух канонических способов (отличающихся ориентацией), а дополнение к дискам всё отправлено в точку \(z\).

Второй шаг: построение гомотопии между модельными отображениями \(f_0’, f_1’\) одинаковой степени. Для этого в цилиндре \(S^n \times [0,1]\) мы соединяем непересекающимися путями все точки из \(f_0^{-1}(y), f_1^{-1}(y)\) (для точки \(y\), которая использовалась при построении модельных отображений \(f_0’, f_1’\) как в первом шаге). При этом важно соединять точки с правильными знаками, как в доказательстве гомотопической инвариантности степени. Так как степени у \(f_0\) и \(f_1\) одинаковые, это удастся сделать. После этого рассматривается тонкая трубчатая окрестность всех этих путей, которую можно запараметризовать как произведение системы путей на \(n\)-мерный диск. В каждом таком диске отображение в сферу определяется как каноническое оборачивание вокруг сферы, а дополнение к трубчатой окрестности отправляется в точку \(z\). Это задаёт гомотопию \(F : S^n \times [0,1] \to S^n\) между \(f_0’\) и \(f_1’\).

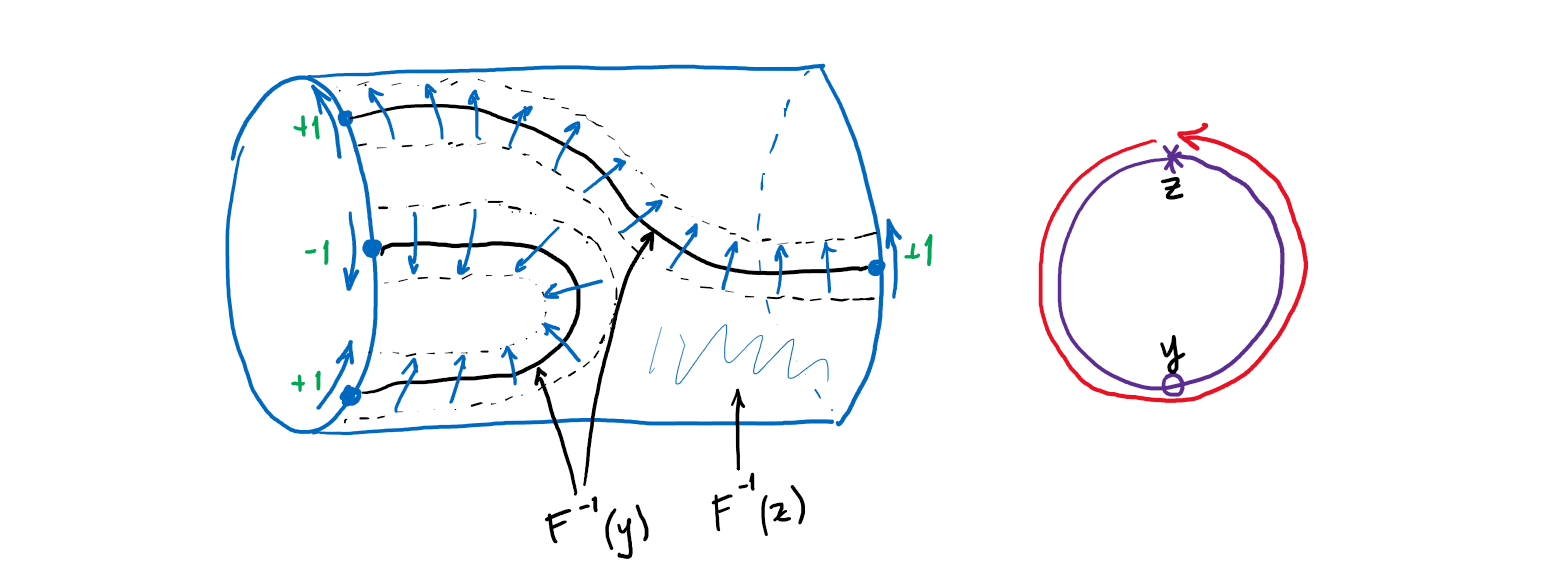
В сухом остатке: если отображения \(f_0, f_1 : S^n \to S^n\) имеют одинаковую степень, то между ними есть гомотопия \(f_0 \sim f_0’ \sim f_1’ \sim f_1\). \(\square\)

Эта теорема обобщается (с таким же доказательством) на отображения из \(n\)-многообразия в \(n\)-сферу.

—Ссылки—

• H. Hopf, Abbildungsklassen n-dimensionaler Mannigfaltigkeiten. Mathematische Annalen (1927).
• Серия постов В. Клепцына от том как топологическая степень помогает считать число вещественных корней многочлена: начало, продолжение, окончание.