Хаусдорфова размерность и её связь с топологической

—18—

Пусть \(X\) — метрическое пространство, а \(d\) — неотрицательное вещественное число (не обязательно целое). Величина \[ \mathcal{H}^d(X) = \lim_{r \to 0} \inf \left\{ \sum_i \delta_i^d ~\middle\vert~ X \text{ можно покрыть шарами } B_{\delta_i}(x_i) \text{ с радиусами } \delta_i < r \right\}. \] называется хаусдорфовой \(d\)-мерой пространства \(X\).

Мера Хаусдорфа при варьировании \(d\) ведёт себя так. Существует пограничное значение \(\hat d\), такое что \(\mathcal{H}^d(X) = +\infty\) для всех \(0 \le d < \hat d\), и \(\mathcal{H}^d(X) = 0\) для всех \(d > \hat d\). Величина \(\hat d\) называется размерностью Хаусдорфа пространства \(X\).

Хаусдорфова размерность, скажем, евклидова куба \([0,1]^n\) согласуется с топологической.

Размерность Хаусдорфа известна в массовой культуре тем, что её удаётся подсчитать для некоторых фрактальных пространств, и результат оказывается дробным. Например, граничная кривая снежинки Коха имеет хаусдорфову размерность \(\log_3 4\), в то время как топологическая её размерность равна \(1\). Западная береговая линия Великобритании настолько изорвана, что приблизительный подсчёт её хаусдорфовой размерности даёт число больше единицы.¹

—19—

Теорема [Szpilrajn, 1937]. Если \(n\)-мера Хаусдорфа метрического компакта \(X\) равна нулю, то \(\text{UW}_{n-1}(X) = 0\). В частности, хаусдорфова размерность \(X\) не меньше топологической размерности.

Доказательство. Идея рассуждения ниже (восходящая, кажется, к Громову) такова: взять мелкое покрытие (неконтролируемой кратности) и модифицировать отображение в нерв так, чтобы его образ стал не более чем \((n-1)\)-мерный, а прообразы точек всё ещё были малыми.

Итак, выберем произвольное открытое покрытие \(X = \bigcup\limits_{i=1}^N U_i\) множествами диаметра меньше \(\varepsilon\), для произвольного фиксированного \(\varepsilon >0\). Построим отображение в нерв явно, примерно как в —16—. Пусть \(\rho\) — число Лебега покрытия, тогда определим \[ \psi_i(x) = \begin{cases} 1, & \text{dist}(x, X\setminus U_i) \ge \rho, \\ \frac{1}{\rho} \text{dist}(x, X\setminus U_i), & \text{dist}(x, X\setminus U_i) < \rho. \end{cases} \]

Строим разбиение единицы: \[ \varphi_i(x) = \frac{\psi_i(x) }{\sum\limits_{j=1}^N \psi_j(x)}. \]

Отображение \(\psi : X \to \mathbb{R}^N\), заданное функциями \(\psi_i\), \(\frac{1}{\rho}\)-липшицево², так как каждая из функций \(\psi_i\) по отдельности \(\frac{1}{\rho}\)-липшицева. Отображение \(\varphi : X \to \triangle^{N-1}\), заданное функциями \(\varphi_i\), \(\frac{1}{\rho}\)-липшицево как композиция \(\psi\) и перенормирования³ \(y \mapsto \frac{y}{\lVert y\rVert_1}\), которое 1-липшицево на образе \(\psi\).

Липшицевость отображения \(\varphi\) среди прочего влечёт, что \(\mathcal{H}^n(\varphi(X)) \le \frac{1}{\rho^n} \mathcal{H}^n(X) = 0\).

Идея доказательства состоит в том, что мы будет индуктивно деформировать \(\varphi\), так чтобы его образ в итоге попал в \((n-1)\)-мерный остов нерва (объединение \((n-1)\)-мерных сиплексов в \(\triangle^{N-1}\)).

Пусть на очередном шаге мы имеем липшицево отображение \(\varphi^{(m)}\), \(n \le m \le N-1\), из \(X\) в \(m\)-мерный остов \(\triangle^{N-1}\). На первом шаге это просто \(\varphi = \varphi^{(N-1)}\). Пусть образ \(\varphi^{(m)}\) задевает относительную внутренность какой-то \(m\)-грани \(F\subset \triangle^{N-1}\). Мы выберем точку \(y\) в относительной внутренности \(F\) вне образа \(\varphi^{(m)}(X)\) и рассмотрим радиальную ретракцию \(\tau_F : F\setminus\{y\} \to \partial F\). Во-первых, такая точка \(y\) существует; из того, что \(\mathcal{H}^n(\varphi^{(m)}(X)) = 0\), следует, что \(\mathcal{H}^m(\varphi^{(m)}(X)) = 0\), и поэтому \(\varphi^{(m)}\) не накрывает всю \(F\). Во-вторых, ограничение \(\tau\) на \(\varphi^{(m)}(X) \cap F\) липшицево с константой, зависящей от \(\text{dist}(y,\partial F) > 0\) и \(\text{dist}(y,\varphi^{(m)}(X)) >0\). Нам не важно конкретное значение этой константы, нам лишь важно, что она есть. Все такие отображения \(\tau_F\) по всем граням \(F\) объединяются в одно отображение \(\tau\) из \(\varphi^{(m)}(X)\) в \((m-1)\)-мерный остов \(\triangle^{N-1}\). Наконец, положим \(\varphi^{(m-1)} = \tau \circ \varphi^{(m)}\). Это отображение липшицево как композиция липшицевых.

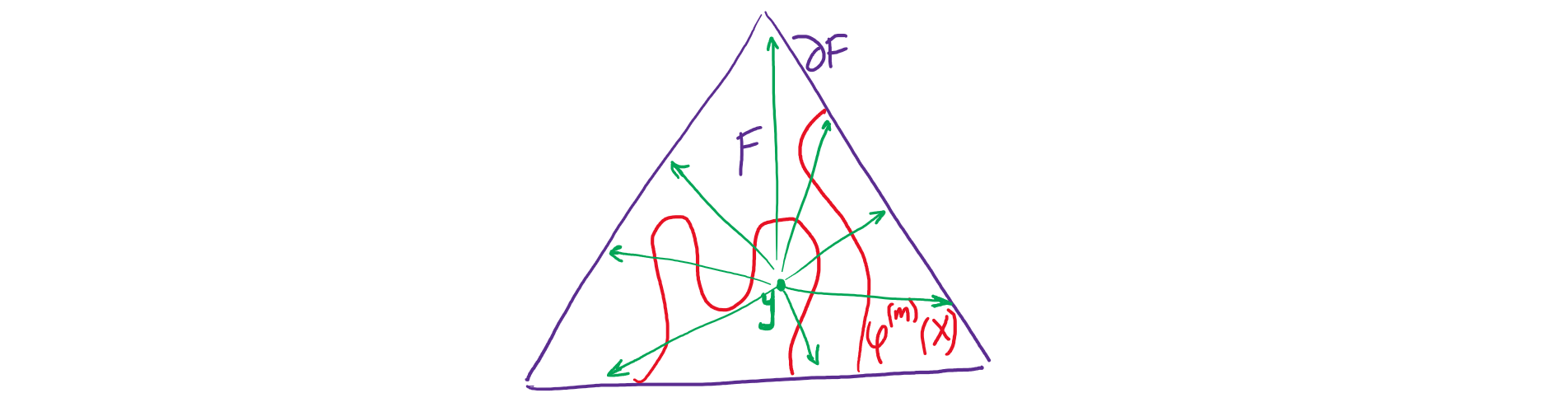
В конечном итоге мы придём к отображению \(\varphi^{(n-1)}\) c не более чем \((n-1)\)-мерным образом. Какие у него слои (прообразы точек)? Про слои исходного отображения \(\varphi\) ясно, что любой из них полностью лежит в одном из \(U_i\), а значит, имеет диаметр меньше \(\varepsilon\). Легко проверить, что это условие сохраняется и после применения всех ретракций \(\tau\), поэтому \(\text{UW}_{n-1}(X) \le \varepsilon\). Повторяя это рассуждение для сколь угодно малого \(\varepsilon > 0\), получаем, что метрическая (и тогда и топологическая) размерность \(X\) не превосходит \(n-1\). \(\square\)

—Ссылки—

• E. Szpilrajn, La dimension et la mesure. Fundameta Mathematicae (1937).
• Набросок доказательства, расшифрованный в этом посте подробно, взят из статьи Гута, который, по-видимому, вдохновлялся идеями Громова.