Топологическая центральная точка

—20—

Нам понадобится наблюдение следующего типа: любое непрерывное отображение из примерно \(md\)-мерного пространства в \(m\)-мерное пространство имеет слой¹, который существенно \(d\)-мерен. Интуитивно может показаться, что нужно уметь доказывать такого рода утверждение с \(m+d\) вместо \(md\), однако — увы! — топологическая размерность ведёт себя крайне неинтуитивно в этом отношении.

Лемма [Gromov, 1988]. Пусть \(n = (m+1)(d+1)\), где \(n,m,d\) — целые неотрицательные числа. Любое непрерывное отображение \(f : X \to Y^m\) из метрического компакта в метризуемое пространство (топологической) размерности \(\le m\) имеет слой \(f^{-1}(y)\) с большим \(d\)-поперечником: \(\text{UW}_d(f^{-1}(y)) \ge \text{UW}_{n-1}(X)\).

Доказательство. Предположим, что \(\sup_y \text{UW}_d(f^{-1}(y)) < \text{UW}_{n-1}(X)\) и зафиксируем \(0 < \varepsilon < \text{UW}_{n-1}(X) - \sup_y \text{UW}_d(f^{-1}(y))\) Для любой точки \(y \in Y\) поперечник слоя \(f^{-1}(y)\) примерно равен поперечнику «утолщённого слоя» \(f^{-1}(U_r(y))\) над малой \(r\)-окрестностью \(y\). Формально говоря, \[ \text{UW}_d(f^{-1}(y)) = \lim_{r \to \infty} \text{UW}_d(f^{-1}(U_r(y))). \] Чтобы это увидеть, можно заметить, что если слой \(f^{-1}(y)\) покрыт какими-то открытыми множествами в \(X\) (с контролируемой кратностью и диаметрами), то те же множества покрывают и утолщённый слой для достаточно малого \(r\). Собирая из таких окрестностей \(U_r(y)\) покрытие компактного пространства \(f(X)\) кратности \(\le m+1\), и рассматривая прообразы этих множеств, получаем покрытие \(X = \bigcup_i U_i\) кратности \(\le m+1\). Для каждого из множеств \(U_i\) верно \(\text{UW}_d(U_i) < \sup_y \text{UW}_d(f^{-1}(y)) + \varepsilon < \text{UW}_{n-1}(X)\). Поэтому существуют открытые покрытия \(U_i = \bigcup_j U_{ij}\) кратности \(\le d+1\) из множеств диаметра меньше \(\text{UW}_{n-1}(X)\). Тогда открытое покрытие \(X = \bigcup_i \bigcup_j U_{ij}\) имеет кратность \(\le (m+1)(d+1)\) и свидетельствует, что \(\text{UW}_{n-1}(X) < \text{UW}_{n-1}(X)\), противоречие. \(\square\)

—21—

Теорема [Karasev, 2010]. Пусть \(n = (m+1)r\), где \(n,m,r\) — целые неотрицательные числа. Любое непрерывное отображение \(f : \triangle^n \to Y^m\) из \(n\)-симплекса в метризуемое пространство (топологической) размерности \(\le m\) имеет слой, задевающий все \(mr\)-грани симплекса.

При \(r=1\) эта теорема превращается в версию ККМ-леммы. Для аффинных отображений в \(\mathbb{R}^m\) получается теорема Радо о центральной точке: для любого облака точек в \(\mathbb{R}^m\) существует такая центральная точка \(y \in \mathbb{R}^m\) (не из облака), что любая гиперплоскость через \(y\) делит точки облака в отношении не хуже \(1:m\).

Для доказательства нам понадобятся две леммы. Первая из них — по сути, единственный топологический ингредиент доказательства. Пусть \(B^n\) обозначает единичный шар пространства \(\mathbb{R}^n\).

Лемма 1.
\[ \text{UW}_{n-1}(B^n) > 0. \]

Доказательство следует из любой версии леммы Шпернера. На самом деле это утверждение можно воспринимать как ещё один аналог инвариантности размерности. Более подробно: в шар можно вписать куб, а его поперечник ненулевой по лемме Лебега о покрытиях. \(\square\)

Лемма 2. Существует симплекс \( \triangle^n \subset \mathbb{R}^n\), удовлетворяющий следующему свойству. Отражения в гипергранях этого симплекса порождают группу \(G\). Образы \(g \cdot \triangle^n\), \(g \in G\), образуют триангуляцию \(\mathbb{R}^n\), и более того, единственный элемент группы, переводящий \(\triangle^n\) в себя, — это единичный элемент группы.²

Доказательство я не провожу подробно и оставляю детали на разбор читателю. Рассмотрим следующее дискретное множество точек: \[ A_n^* = \left\{(x_0,x_1,\ldots,x_n) \in \mathbb{Z}^{n+1} ~\middle\vert~ \sum_{i=0}^n x_i = 0, ~ x_0 \equiv x_1 \equiv \ldots \equiv x_n \pmod{n+1}\right\}. \] Это множество живёт в гиперплоскости \(\sum x_i = 0\), поэтому будет считать, что дело происходит в \(\mathbb{R}^n\). Рассмотрим триангуляцию Делоне множества \(A_n^*\): набор вершин образует клетку триангуляции, если есть сфера, на которой лежит весь этот набор, и внутри которой нет никаких вершин \(A_n^*\). Эта триангуляция состоит из конгруэнтных симплексов, и группа, порождённая отражениями в их гипергранях, действует свободно на симплексах. \(\square\)

Доказательство теоремы Карасёва.

Можно считать, что \(f : \triangle^n \to Y^m\) задано на симплексе из леммы 2. Предположим, для любой точки \(y \in Y\) найдётся \(mr\)-грань \(F_y \subset \triangle^n\), которую не задевает \(f^{-1}(y)\). Пусть \(F_y^\vee\) — \((r-1)\)-грань, образованная всеми вершинами \(\triangle^n\), не входящими в \(F_y\). Любая точка \(x \in \triangle^n\) может быть представлена как \(x = t \xi + (1-t) \eta\), \(t \in [0,1]\), \(\xi \in F_y\), \(\eta \in F_y^\vee\), причём \(t\) определяется однозначно, и если \(t<1\), то \(\eta\) тоже определяется однозначно.³ Отображение \(p : x \mapsto \eta\) корректно определено на \(\triangle^n \setminus F_y\), непрерывно и двигает каждую точку на расстояние меньше \(\text{diam }\triangle^n\).

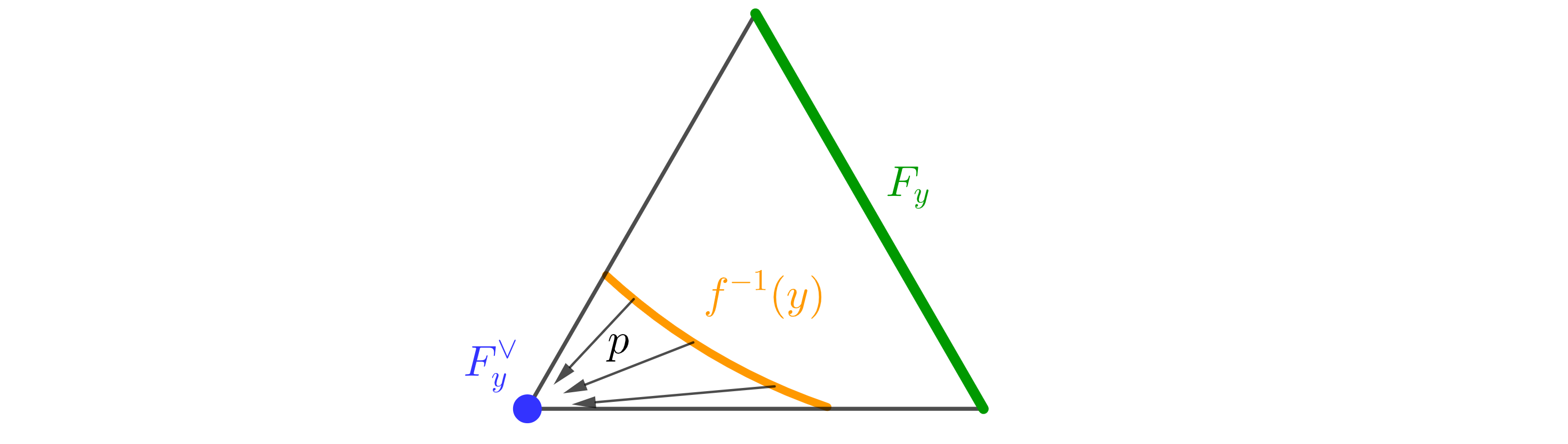
Воспользуемся леммой 2, чтобы продолжить картинку с симплекса на всё \(\mathbb{R}^n\). А именно, определим \(\tilde f: \mathbb{R}^n \to Y^m\) как \(G\)-инвариантное⁴ продолжение \(f : \triangle^n \to Y^m\), и определим \(\tilde p : \tilde f^{-1}(y) \to G \cdot F_y^\vee\) как \(G\)-эквивариантное⁵ продолжение \(p : f^{-1}(y) \to F_y^\vee\).

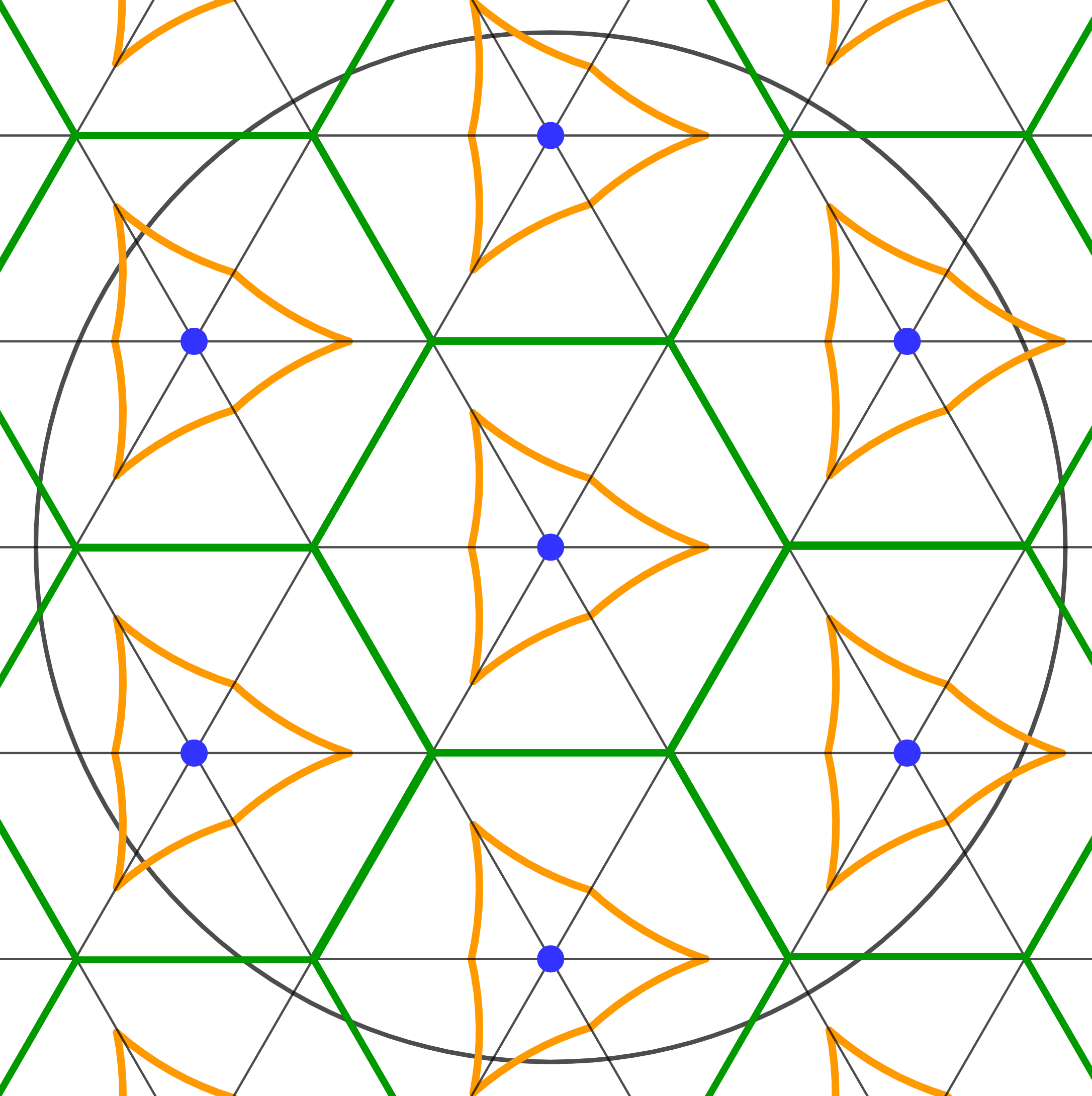
Выберем большой радиус \(R > \frac{2 \text{ diam } \triangle^n}{\text{UW}_{n-1}(B^n)}\) и положим \(X \subset \mathbb{R}^n\) равным шару радиуса \(R\). Тогда ограничение \(\tilde p\vert_X\) свидетельствует, что \(\text{UW}_{r-1}(\tilde f^{-1}(y) \cap X) \le 2 \text{ diam }\triangle^n\). С другой стороны, применение леммы Громова к отображению \(\tilde f\vert_X : X \to Y^m\) показывает, что должна существовать точка \(y\), для которой \[ \text{UW}_{r-1}(\tilde f^{-1}(y) \cap X) \ge \text{UW}_{n-1}(X) = R \cdot\text{UW}_{n-1}(B^n) > 2 \text{ diam }\triangle^n, \] противоречие. \(\square\)

—Ссылки—

• Р. Карасёв предложил два доказательства топологической теоремы о центральной точке, “вещественное торическое” и “комплексное торическое”, оба существенно труднее, чем рассуждение здесь.