Лекция проходила вживую, видеозаписи с неё нету. Первая часть лекции была посвящена обзору курса, а вторая часть законспектирована ниже.

—Пересказ—

Теорема [Dehn, 1903]. Если прямоугольник допускает разрезание на квадраты, то отношение его сторон рационально.

Набросок доказательства. Любому замощению прямоугольника прямоугольниками удобно поставить в соответствие электрическую схему из резисторов по следующему правилу. Прямоугольник замощения с горизонтальной стороной \(U\) и вертикальной стороной \(I\) становится резистором сопротивления \(U/I\). Резисторы соединяются проводом, если соответствующие прямоугольники смежны вдоль вертикального отрезка. Правая и левая сторона большого прямоугольника соединены с клеммами батарейки единичного напряжения.

Электрическая аналогия

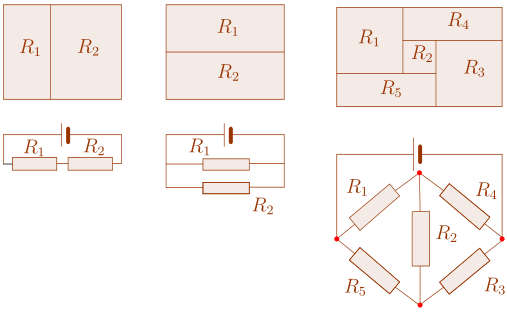
Проверяется, что токи и напряжения в этой сети, соответствующие вертикальным и горизонтальным сторонам прямоугольников, удовлетворяют обоим правилам Кирхгофа. А значит, система Кирхгофа, построенная по такой сети, рассматриваемая как линейная система уравнений относительно токов, имеет нетривиальное решение.

Наблюдение 1. Пусть граф электрической сети имеет \(V\) вершин, \(E\) рёбер (резисторы + батарейка), \(F\) ограниченных граней. Тогда система Кирхгофа может быть записана как \(V-1+F\) уравнений (\(V-1\) первых правил и \(F\) вторых) относительно \(E\) неизвестных токов. По теореме Эйлера \(V-1+F = E\), то есть матрица системы квадратная.

Наблюдение 2. Система Кирхгофа имеет не более одного решения. В противном случае, вычитая два решения, мы получает нетривиальную систему токов в сети с нулевой батарейкой. Такое “фантомное” решение противоречит второму правилу Кирхгофа, потому что в такой сети можно найти циркуляцию тока вдоль замкнутого контура.

Наблюдение 3. Решение системы Кирхгофа, выписанное по методу Гаусса или Крамера, рационально выражается через сопротивления резисторов. В случае теоремы Дена, все сопротивления единичные, и суммарный ток в сети (вертикальная сторона большого прямоугольника) вынужденно рациональный. \(\square\)

—Cсылки—