Задачи

Пусть \(G = (V, E)\) — неориентированный граф. Определим алгебраические операции на ориентированных циклах. Каждому ориентированному циклу \(C\) сопоставим вектор в \(\mathbb{Z}^{|E|}\), состоящий из плюс-минус единиц в тех позициях, которые отвечают рёбрам цикла. Чтобы выбрать знаки, заранее зафиксируем вспомогательную ориентацию на рёбрах графа; если ребро из \(C\) согласовано с ней, напишем \(+1\), иначе \(-1\). Циклы, представленные таким образом, можно складывать как вектора в \(\mathbb{Z}^{|E|}\).

• Пусть \(G\) — связный граф, а \(T\) — остовное дерево в нём (связный подграф без циклов). Рассмотрим все циклы в \(G\), возникающие, если к \(T\) добавить одно дополнительное ребро, и назовём их базисными. Докажите, что любой ориентированный цикл в графе \(G\) можно представить в виде суммы базисных (произвольно ориентированных).

• Пусть \(G\) — планарный граф, нарисованный на плоскости. Рассмотрим все циклы в \(G\), ограничивающие внутренние области нарисованного графа, и назовём их базисными. Докажите, что любой ориентированный цикл в графе \(G\) можно представить в виде суммы базисных (произвольно ориентированных).

Можно ли разрезать куб на меньшие кубы попарно различных размеров?

Пусть \(A\) и \(B\) — два прямоугольника. Из прямоугольников, равных \(A\), сложили прямоугольник, подобный \(B\). Докажите, что из прямоугольников, равных \(B\), можно сложить прямоугольник, подобный \(A\).

Можно ли разрезать квадрат на прямоугольники (горизонтальные и вертикальные) с отношением сторон

• \(\sqrt{2}\)?

• \(\frac{3+\sqrt{3}}{2}\)?

• \(1+\sqrt{2}\)?

В цепи из резисторов в нескольких узлах (возможно, более чем в двух) зафиксировали определённые заданные потенциалы. Докажите, что ток в цепи установится однозначно.

• Операция принимает на вход связную планарную цепь из резисторов, нарисованную на плоскости и подключённую к двум клеммам на границе внешней грани, и возвращает цепь той же природы.
• Двойственная цепь состоит из такого же количества резисторов, что и исходная, причём их сопротивления обратны сопротивлениям резисторов исходной цепи, и итоговое сопротивление всей двойственной цепи тоже обратно сопротивлению исходной цепи.

Связный граф \(G = (V, E)\) реализовали при помощи идеальных упругих резинок (рёбра представлены резинками, концы которых склеены так же, как рёбра сходятся в графе). Резинки удовлетворяют закону Гука: сила натяжения пропорциональна длине (жёсткость у всех резинок одинаковая). Два узла графа прибили гвоздями на расстоянии \(1\) друг от друга. Какая сила натяжения действует на каждый из гвоздей?

При помощи матричной теоремы о деревьях вычислите эффективное сопротивление между соседними вершинами додекаэдра (рассматривается каркас додекаэдра, в котором каждое ребро имеет единичное сопротивление).

Пусть \(L\) — лапласиан графа на \(n\) вершинах, \(J\) — матрица, состоящая из единиц, а \(\tau\) — количество остовных деревьев в графе. Докажите, что \(\det (L+J) = n^2 \tau\).

Пусть \(e,f\) — различные рёбра графа \(G\). Докажите, что \(\tau(G) \tau(G\setminus \{e,f\}) \le \tau(G\setminus \{e\})\tau(G\setminus \{f\})\).

Сведите задачу подсчёта числа разбиений доски \(2n \times 2m\) на доминошки к задаче подсчёта количества остовных деревьев в некотором графе на \(mn+1\) вершинах.

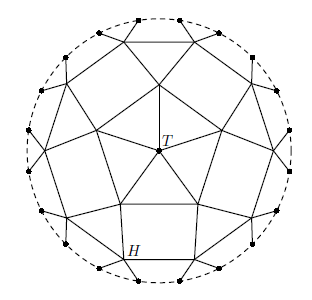
На рисунке ниже представлена туристическая карта Парижа. Пьяный турист выходит из отеля \(H\) и случайно перемещается по улицам. Найдите вероятность того, что он достигнет Триумфальной арки \(T\) раньше, чем доберётся до окраины города.

Утолщённый \(n\)-диамант получается из обычного ацтекского \(n\)-диаманта путём вставки дополнительного горизонтального ряда из \(2n\) клеточек между средними рядами. Докажите, что количество разбиений такого диаманта на доминошки выражается через числа Деланнуа. Эти числа определяются как количество способов, которыми хромой шахматный король может дойти из левого нижнего угла квадратной шахматной доски в правый верхний угол; хромой король может ходить только направо, вверх, или по диагонали направо-вверх.

Пусть \(a_1 < \ldots < a_n\) и \(b_1 < \ldots < b_n\) — натуральные числа. Докажите, что детерминант \[ \begin{vmatrix} {a_1 \choose b_1} & \cdots & {a_1 \choose b_n}\\ \vdots & \ddots & \vdots\\ {a_n \choose b_1} & \cdots & {a_n \choose b_n} \end{vmatrix} \] неотрицателен, и что он обнуляется если и только если \(a_i < b_i\) для некоторого \(i\). (Подсказка: при помощи трюка Линдстрёма проинтерпретируйте этот детерминант в терминах систем клеточных путей.)

Трёхмерная диаграмма Юнга определяется естественным образом как фигура из кубиков, сложенных в положительный координатный октант трёхмерного пространства, вместе с любым своим кубиком с координатами \((i,j,k)\) содержащая все кубики с координатами \((\le i, \le j, \le k)\). Докажите формулу Макмагона для числа трёхмерных диаграмм, вписанных в параллелепипед размера \(a \times b \times c\): \[ \prod_{i=1}^a \prod_{j=1}^b \prod_{k=1}^c \frac{i+j+k-1}{i+j+k-2}. \] (Подсказка: горизонтальные срезы трёхмерной диаграммы на разных высотах могут быть проинтерпретированы как вложенная система двумерных диаграмм, а также система непересекающихся клеточных путей.)

Сколько стандартных таблиц может быть вписано в диаграмму Юнга, представляющую собой прямоугольник \(2 \times n\)?

Опишите группу симметрий октаэдра; группу вращений (симметрий, сохраняющих ориентацию) октаэдра; группу симметрий додекаэдра; группу вращений додекаэдра.

Докажите, что группы \(A_3\) и \(D_3\) (из классификации Кокстера) изоморфны.

В игре Before we leave можно увидеть сферу, замощённую шестиугольниками. Где подвох?

Пусть \(G = \langle s_1, \ldots, s_N \vert R \rangle\) — группа Кокстера, соотношения в котрой заданы матрицей \((m_{ij})_{i,j = 1}^{N}\). Пусть \(V\) — вещественное векторное пространство размерности \(N\) с базисом \(e_1, \ldots, e_N\). Определим “псевдоскалярное” произведение на базисных векторах так: \(\langle e_i, e_j\rangle = -\cos \frac{\pi}{m_{ij}}\); при этом полагаем \(\cos \frac{\pi}{\infty} = 1\). Продолжим это произведение билинейно на всё пространство. Оно не обязано оказаться положительно определённым, но формально можно попытаться рассмотреть линейное преобразование (“отражение”) \(x \mapsto x - 2\langle x,e_i\rangle e_i\). Докажите, что такие отражения представляют группу \(W\) в пространстве \(V\); иными словами, проверьте, что эти отражения удовлетворяют соотношениям Кокстера. (Вообще говоря, полученное представление может оказаться неточным, то есть оно может отправить какой-то нетривиальный элемент группы \(W\) в тождественное преобразование.)

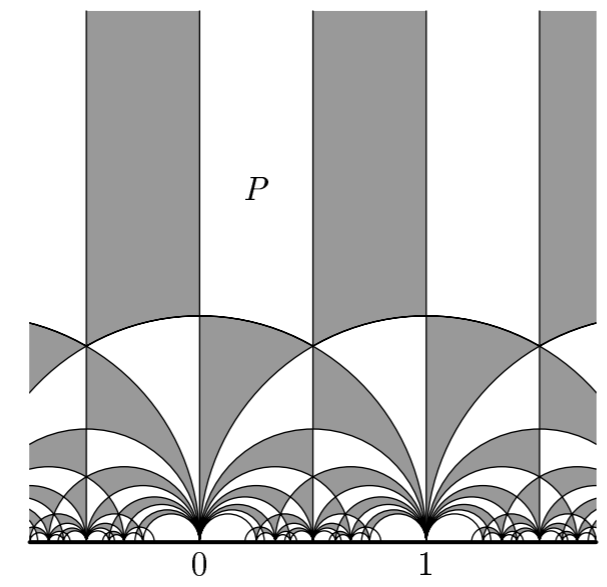
На верхней комплексной полуплоскости \(\text{Im } z > 0\) рассматривается действие группы, состоящей из преобразований вида \[ z \mapsto \frac{az+b}{cz+d}, \; a,b,c,d \in \mathbb{Z},\; ad-bc = 1, \] и преобразований вида \[ z \mapsto \frac{a\bar z+b}{c\bar z+d}, \; a,b,c,d \in \mathbb{Z}, \; ad-bc = -1. \] Докажите, что эта группа порождается преобразованиями \[ z \mapsto -\bar z, \; z \mapsto 1-\bar z, \; z \mapsto \frac{1}{\bar z}. \] Какие между ними соотношения? (Подсказка: проверьте что параметры \(a,b,c,d\) при композиции преобразований меняются как матрицы при перемножении; соответствующее утверждение про матрицы можно доказать при помощи алгоритма Евклида. Смысл этой задачи — иллюстрация важной группы отражений плоскости Лобачевского.)

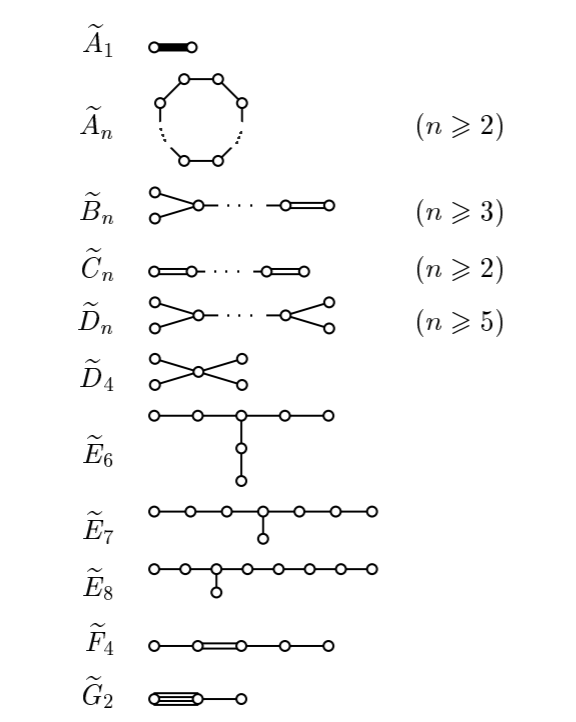
Пусть ненулевые вектора \(v_1, \ldots, v_N \in \mathbb{R}^n\) образуют тупоугольную систему в том смысле, что скалярное произведение любых двух различных векторов неположительно. Докажите, что либо эта система разложима (распадается в объединение двух, лежащих в ортогональных подпространствах), либо \(N \le n+1\). (Эта лемма возникает в классификации неразложимых аффинных групп отражений. Из леммы следует, что фундаментальная камера Вейля неразложимой аффинной группы отражений — симплекс. Стабилизатор каждой его вершины — конечная группа отражений, поэтому система внутренних нормалей к стенкам камеры характеризуется так: её матрица Грама вырождена, но любой главный минор её положителен. Классификация таких матриц с элементами вида \(-\cos(\pi/m_{ij})\) приводит к следующему списку схем Кокстера аффинных групп.)

Докажите, что параллельными транслятами пермутоэдра \(P_{n-1}\) можно замостить \(\mathbb{R}^{n-1}\). Для этого проверьте, что пермутоэдр (с точностью до преобразования подобия) есть множество точек, которые ближе к нулю чем к другим точкам решётки \(A_{n-1}^* = \{(x_1, \ldots, x_n) \in \mathbb{Z}^{n} ~\vert~ \sum x_i = 0, x_1 \equiv \ldots \equiv x_n \pmod{n}\}\), рассматриваемой как подмножество в \(\{(x_1, \ldots, x_n) \in \mathbb{R}^{n} ~\vert~ \sum x_i = 0\} \cong \mathbb{R}^{n-1}\).