—Тезисы—

Рассечём циклический зонотоп \(Z_{n,3}\), подразбитый на параллелепипеды, “горизонтальными” плоскостями на высоте \(0, 1, 2, \ldots, n\), т.е. плоскостями вида \(H_k = \{(k,x_2,x_3) ~\vert~ x_2,x_3 \in \mathbb{R}\}\), \(k \in \{0, 1, 2, \ldots, n\}\). В случае \(n=3\) мы увидим два тривиальных сечения, и два треугольных сечения, назовём их белым (\(H_1\)) и чёрным (\(H_2\)). В случае общего \(n\) во все нетривиальных сечениях мы видим \(n\)-угольник, разбитый на треугольники двух видов, белые и чёрные (в зависимости от того, получаются они как нижнее или как верхнее сечение соответствующего тайла). Маркируем вершины \(\sum\limits_{i \in I} v_i\) зонотопального разбиения подмножествами \(I \subset [n]\). Тогда белые треугольники маркированы тройками вида \(I \cup \{a\}, I \cup \{b\}, I \cup \{c\}\), а чёрные — \(I \cup \{a,b\}, I \cup \{a,c\}, I \cup \{b,c\}\).

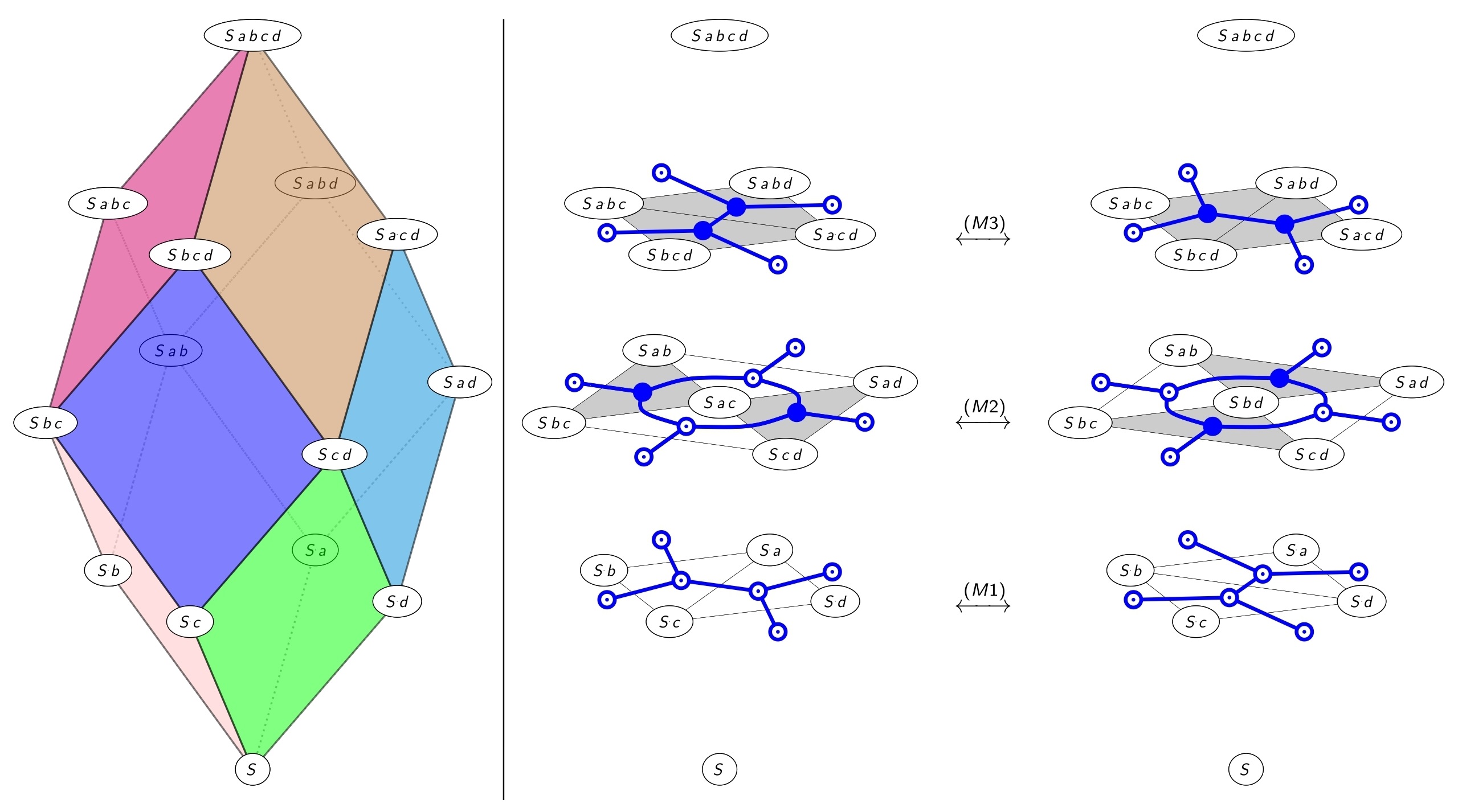
Плабиками типа \((n,k)\) назовём всевозможные чёрно-белые триангуляции в слое \(H_k\). Флипы плабиков происходят из зонотопальных флипов, и посему бывают трёх видов; их можно увидеть в сечениях двух различных разбиений ромбододекаэра \(Z_{4,3}\).

Флипы плабиков

Грассманово ожерелье — последовательность множеств \(I_1, \ldots, I_n \in {[n] \choose k}\), такая что для любого \(i\) если \(i \in I_i\), то найдётся \(j\), для которого \(I_{i+1} = (I_i \setminus \{i\}) \cup \{j\}\), а если \(i \notin I\), то \(I_{i+1} = I_i\) (индексация циклическая по модулю \(n\)). Украшенная перестановка — перестановка, у которой неподвижные точки покрашены в два цвета. Между ожерельями внутри \([n]\) и украшенными перестановками на множестве \([n]\) есть естественная биекция. Для ожерелья \(I_1, \ldots, I_n \in {[n] \choose k}\) в первом приближении это отображение \(i \mapsto j\) из определения ожерелья. В случае \(I_{i+1} = I_i\) мы красим неподвижную точку \(i \mapsto i\) в один их двух цветов в зависимости от того, \(i \in I\) или \(i \notin I\). Спиральность соответствующей украшенной перестановки по определению положена \(k\).

Внутри плабика типа \((n,k)\) можно поискать ожерелья; более точно, ломаные вдоль рёбер триангуляции, вершинные метки которых образуют ожерелье (в вершинах разрешается “топтаться”, если в соответствующей перестановке есть неподвижные точки). Например, граница всегд плабика — ожерелье с украшенной перестановкой \(\pi^{(n,k)} : i \mapsto i+k \pmod{n}\). Оказывается, любое ожерелье можно найти внутри какого-то плабика типа \((n,k)\) (и не в одном). Более того, ожерелье всегда обходит какое-то односвязное объединение треугольников и рёбер плабика; назовём это объединение плабиком типа \(\pi^:\), где \(\pi^:\) — украшенная перестановка данного ожерелья. Плабики типа \((n,k)\) суть плабики типа \(\pi^{(n,k)}\).

Маршрутом внутри плабика называется путь, начинающийся и заканчивающийся на внешних ребрах плабика, и переходящий между треугольниками по правилу “в белом треугольнике выбираем путь налево, в чёрном — направо”. Система маршрутов изо всех рёбер определяет маршрутную перестановку плабика, которая совпадает с украшенной перестановкой граничного ожерелья.

А. Постников вводил плабики в двойственном сеттинге — как графы. Наше определение двойственно приведённым тривалентным плабикам Постникова. Эквивалентность оригинального определения и зонотопального показал П. Галашин.

—Cсылки—