Тизер курса + теорема Липтона–Тарьяна

10 Feb 2023

Тизер курса

Пусть $M^n$ — $n$-мерное пространство, в котором мы умеем измерять длины кривых и $n$-мерные объёмы; например, риманово многообразие (значение этих слов мы обсудим позже). Систолой $M$ назовём длину кратчайшей замкнутой кривой в $M^n$, которую нельзя непрерывно продеформировать внутри $M$, так чтобы стянуть её в точку. Обозначение: $\text{sys }M^n.$ Исторически первое систолическое неравенство принадлежит Карлу (Чарльзу) Лёвнеру.

Теорема [Loewner, 1949]. Существует константа $c$, такая что для любой римановой метрики на двумерном торе $T^2$ выполнено систолическое неравенство \(\text{sys }T^2 \le с \sqrt{\text{area }T^2}.\)

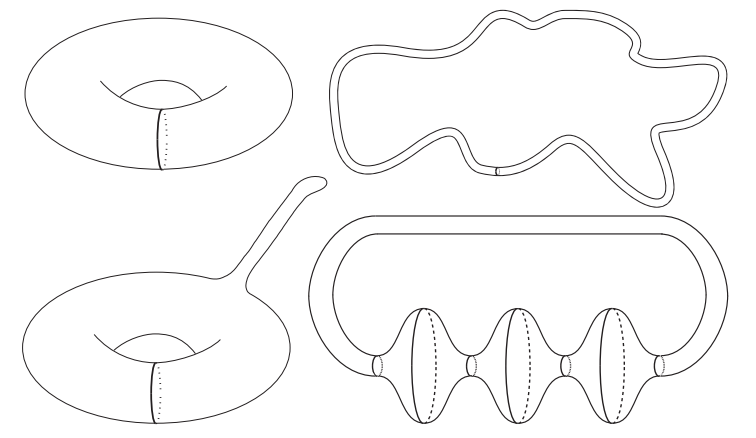
Вместо уточнения того, что такое “риманова метрика”, я оставлю здесь рисунок нескольких торов, вложенных в $\mathbb{R^3}$. Должно быть интуитивно понятно, как определяются длины и площади на этих поверхностях, и неравенство Лёвнера нетривиально даже для таких торов. Лёвнер на самом деле доказал больше: он установил неулучшаемое значение константы $c$.

Метрические торы

В течение семестра мы обсудим (и докажем) два больших результата, обобщающих неравенство Лёвнера в разных направлениях.

(1) Можно задать аналогичный вопрос для $n$-мерного тора, пространства, которое топологически устроено как произведение $n$ окружностей, а метрически может быть устроено сколь угодно сложно.

Теорема [Gromov, 1983]. Существует константа $c_n$, зависящая только от размерности, такая что для любой римановой метрики на $n$-мерном торе $T^n$ выполнено систолическое неравенство $\text{sys }T^n \le с \sqrt[n]{\text{vol }T^n}$.

Миша Громов доказал систолическое неравенство для гораздо более широкого класса пространств, включающего не только торы, но и, например, все двумерные поверхности, кроме сферы.

(2) Если систолическое неравенство Громова для двумерных поверхностей объединить с результатом Кристофера Кроука для двумерных сфер, то получится следующее неравенство.

Теорема [Gromov, 1983 + Croke, 1988]. Существует константа $c$, такая что на любой двумерной поверхности $\Sigma$ (с любой римановой метрикой) существует замкнутая геодезическая кривая длины не больше $с \sqrt{\text{area }\Sigma}$.

Геодезическая — это кривая, локально минимизирующая длину. Другими словами, если на поверхность посалить крошечного муравейчика и попросить его пойти “прямо”, то его траектория будет геодезической. Аналогичное неравенство для трёхмерных пространств — широго открытая гипотеза.

Неравенство для кратчайших геодезических не является буквально систолическим, и название курса немного фигурально в том смысле, что мы будем обсуждать много разных метрических инвариантов пространств, по духу похожих на систолы.

Теорема Липтона–Тарьяна

Один из таких “околосистолических” инвариантов — кратчайшая длина кривой, которая разрезает данную поверхность на куски, каждый из которых имеет площадь, скажем, не более 75% от площади всей поверхности. Следующая теорема — дискретный аналог оценки длины такой кривой. Неформально она утверждает, что планарный граф — плохой экспандер (это слово мы обсудим позже).

Теорема [Lipton–Tarjan, 1979]. Любой планарный граф $G = (V,E)$ на $n$ вершинах содержит множество $S \subset V$ размера $|S| < 2\sqrt{n}$, такое что любая связная компонента дополнения $G \setminus S$ содержит не более $3n/4$ вершин.

Схема доказательства [Miller–Teng–Thurston–Vavasis, 1979].

Ингредиент 1. Любое конечное множество точек $X \subset \mathbb{R}^d$ имеет “медиану”, то есть существует точка $c \in \mathbb{R}^d$, такая что любое замкнутое полупространство, содержащее $c$, содержит хотя бы $\frac{|X|}{d+1}$ точек множества $X$. Это утверждение, называемое теоремой Радо, легко вывести из теоремы Хелли про пересечение выпуклых множеств. А именно, рассмотрим все полупространства, содержащие хотя бы $\frac{|X|}{d+1}$ точек облака $X$ (и пересечём для верности их с большим шаром, содержащим всё $X$). Любые $d+1$ из этих множеств пересекаются, поэтому все они имеют общую точку, которая и есть “медиана”.

Ингредиент 2. Любой планарный граф можно реализовать касаниями кругов на плоскости. Этот факт — трудная теорема, принадлежащая Кёбе, и мы обсудим её в следующий раз.

Теорема Кёбе

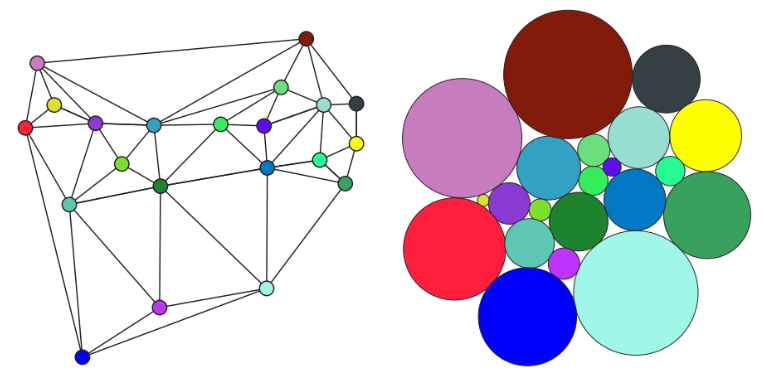
При помощи стереографической проекции представление графа семейством кругов на плоскости можно превратить в представление графа семейством сферических шапочек на сфере. Понятно, что такое представление не единственно. Например, перед тем как стереографически проектировать плоскую картинку на сферу, можно эту картинку подвигать или гомотетично раздуть/сдуть. Полученные таким образом сферические картинки переводятся друг в друга преобразованиями Мёбиуса.

Ингредиент 3. Топологический аргумент в стиле теоремы Брауэра о неподвижной точке позволяет подобрать такое представление графа на сфере, для которого центр сферы явлется “медианой” для множества центров сферических шапочек.

Ингредиент 4. Случайная плоскость через центр сферы пересечёт (в смысле матожидания) не более $2\sqrt{n}$ шапочек, и это множество можно взять в качестве $S$. \(\square\)

Детали этого доказательства будут восполнены позже.

Cсылки