Геодезические на сфере

21 Apr 2023

Геодезические

Кривая $\gamma : [0,1] \to M$ на компактном римановом многообразии $M$ называется геодезической, если она локально минимизирует функционал длины, то есть для любых достаточно близких $t < t’$ отрезок $\gamma\vert_{[t,t’]}$ — кривая кратчайшей длины между $\gamma(t)$ и $\gamma(t’)$. Любые две точки на связном многообразии можно соединить кратчайшей геодезической, как следует из рассуждения типа Картана–Адамара ниже. Геодезическая оказывается гладкой, её можно параметризовать натурально (длиной дуги), и тогда производная в каждой точке будет единичным касательным вектором. Альтернативное определение геодезической можно дать в терминах ковариантной производной на римановом многообразии (ковариантное ускорение геодезической кривой равно нулю; иными словами, геодезическая — это траектория свободной частицы, путешествующей внутри многообразия), но мы его не обсудим. В рассуждениях ниже нам понадобится стандартный факт про римановы многообразия: для любого компактного многообразия найдётся маленькое число $\epsilon$ такое, что любые две точки на расстоянии $\le \epsilon$ могут быть соединены единственной кратчайшей геодезической, которая зависит непрерывно от своих концов, а квадрат длины этой геодезической — гладкая функция концов (для знатоков: в качестве $\epsilon$ можно взять радиус инъективности). Другой стандартный факт: из любой точки $p \in M$ в любом направлении $v \in T_p M$ можно испустить короткий отрезок геодезической с начальной скоростью $v$ (это можно вывести из задачи Коши для дифференциального уравнения “ковариантное ускорение равно нулю”).

Замкнутая геодезическая $\gamma : S^1 \to M$ определяется аналогично. Тождественное отображение окружности в одну точку $M$ называется тривиальной замкнутой геодезической. В 1951-м году Люстерник и Фет доказали, что на любом компактном римановом многообразии существует нетривиальная замкнутая геодезическая при помощи методов теории Морса.

Для неодносвязного $M$ ($\pi_1(M)$ нетривиальна) замкнутую геодезическую можно найти при помощи метода, восходящего к Картану и Адамару. Мы можем стартовать с произвольной нестягиваемой петли и стягивать её (как если бы она была резинкой, стремящейся сократить свою длину), пока она не станет кратчайшей в своём гомотопическом классе. Чтобы строго доказать существование минимума, удобно рассмотреть другой гладкий функционал с тем же минимумом (вместо негладкого функционала длины). Этого будет функционал энергии (квадратичной длины), который мы введём следующим образом. Пусть $\mathcal{P}_N M$ — пространство геодезических $N$-угольников $p_1 \dots p_N \subset M$ с дополнительным условием $\sum\limits_{i=1}^N \text{dist}(p_i, p_{i+1})^2 < \epsilon^2$ (нумерация циклическая, $p_{N+1} = p_1$). Иными словами, на каждой петле из $\mathcal{P}_N M$ отмечено $N$ вершин, и на отрезках между любыми двумя их них кривая проходит вдоль кратчайшей геодезической. Любая спрямляемая замкнутая кривая может быть непрерывно продеформирована в многоугольник для достаточно большого $N$. Для этого нужно расставить вершины на расстоянии $< \epsilon$ вдоль кривой, а после этого на каждом сегменте применить гомотопию как на следующем рисунке.

Деформация геодезической

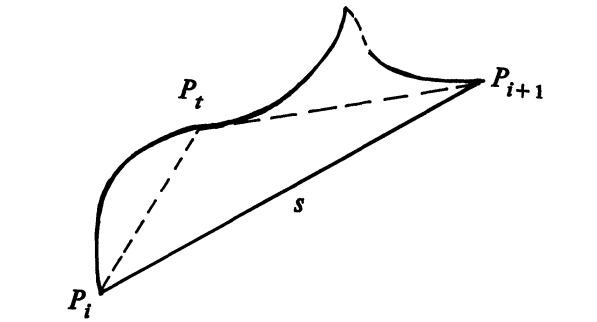
Если дуга между $p_i$ и $p_{i+1}$ запараметризована параметром $t \in [0,1]$, то для каждого $t$ можно рассмотреть кривую, которая идёт от $p_i$ до $p(t)$ вдоль исходной петли, а от $p(t)$ до $p_{i+1}$ — вдоль кратчайшей геодезической между этими двумя точками. Это семейство кривых по всем $t$ даёт гомотопию между исходной петлёй и геодезическим многоугольником.

Теперь рассмотрим гладкий функционал энергии на $\mathcal{P}_N M$:

\[E(p_1, \ldots, p_N) = \sum_{i=1}^N \text{dist}(p_i, p_{i+1})^2.\]

Его минимум достигается на замкнутой геодезической, как следует из следующей леммы.

Лемма. Критические точка функционала энергии — замкнутые геодезические.

Доказательство. Пусть $\gamma$ — кратчайшая геодезическая между точками $p$ и $q$ в натуральной параметризации (параметризации длиной дуги). Её производная $\gamma’$ есть единичный касательный вектор к кривой, включая односторонние производные в концевых точках $\gamma’_+\vert_p$ и $\gamma’_-\vert_q$. Дифференциал квадрата расстояния $\text{dist}(p,q)^2$, вычисленный в касательных векторах $\xi_p \in T_pM, \xi_q \in T_qM$, равняется

\[d \; \text{dist}^2 (\xi_p, \xi_q) = 2\; \text{dist}(p,q) \cdot \left( \langle \gamma'_-\vert_q, \xi_q \rangle - \langle \gamma'_+\vert_p, \xi_p \rangle \right).\]

Тогда дифференциал энергии, вычисленный в касательных векторах $\xi_i \in T_{p_i}M$, равняется

\[d E (\xi_1, \ldots, \xi_N) = 2\; \text{dist}(p,q) \sum_{i=1}^N \left\langle \xi_i, \text{dist}(p_{i-1}, p_i) \cdot \gamma'_-\vert_{p_i} - \text{dist}(p_i, p_{i+1}) \cdot \gamma'_+\vert_{p_i} \right\rangle.\]

Если $dE = 0$, то вектора $\text{dist}(p_{i-1}, p_i) \cdot \gamma’_-\vert_{p_i}$ и $\text{dist}(p_i, p_{i+1}) \cdot \gamma’_+\vert_{p_i}$ равны, откуда следует, что стороны многоугольника склеиваются гладко в замкнутую геодезическую. \(\square\)

Из этого аргумента следует, что систола неодносвязного компактного многообразия достигается на какой-то замкнутой геодезической.

Для односвязного $M$ ($\pi_1(M)$ тривиальна) найти замкнутую геодезическую значительно труднее, и именно в этом содержание теоремы Люстерника–Фета. Ниже мы продемонстрируем идею доказательства для случая сферы $S^2$. Для многомерных односвязных многообразий идея та же, но требуется понимание некоторых фактов из гомотопической теории.

Минимакс Биркгофа

Докажем, что на любой римановой двумерной сфере есть замкнутая геодезическая минимаксным методом Биркгофа. Любая отдельно взятая петля на сфере стягиваема, однако можно взять целое однопараметрическое семейство петель на сфере, которые будут “в совокупности нестягиваемы”, и уже пытаться укоротить все петли в этом семействе.

Разрезанием сферы на окружности назовём непрерывное отображение $S^2 \to [0,1]$, у которого прообраз любой точки гомеоморфен либо точке, либо окружности, либо “восьмёрке”, либо конечному объединению таковых. “Восьмёрка” при этом подразумевается самопересекающейся окружностью. Самый простой случай разрезания — когда восьмёрки не встречаются, и сфера отображается в отрезок так, что прообразы его концов — точки, а все остальные прообразы — окружности; назовём такие разрезания простыми.

Заметанием римановой сферы $(S^2,g)$ окружностями назовём следующий набор данных.

  • Во-первых, нам нужна отдельная сфера $S^2$, разрезанная на окружности посредством отображения в граф $p: S^2 \to Y$.

  • Во-вторых, нам нужно почти всюду гладкое отображение $f: S^2 \to S^2$ степени $1$, где левая сфера оснащена разрезанием $p$, а правая сфера оснащена римановой метрикой $g$. Отображение $f$ переносит разрезание $\{p^{-1}(y)\}_{y \in Y}$ с левой сферы на правую сферу, и слои $f(p^{-1}(y))$, $y \in Y$, заметают правую сферу.

  • Можно определить длину слоя $f(p^{-1}(y))$ в заметании при помощи метрики $g$. Тут есть нюанс: если образ $f(p^{-1}(y))$ проходит по некоторым участкам многократно, длину нужно считать с кратностью. Более формально, длина слоя $f(p^{-1}(y))$ определяется как длина $p^{-1}(y)$ в метрике $f^* g$, обратном образе $g$.

  • Назовём заметание простым, если оно является образом простого разрезания.

Укорачивание кривых по Биркгофу — процесс, который непрерывно деформирует замкнутую кривую $\gamma: S^1 \to (S^2,g)$ так, что длина в процессе не увеличивается, а в пределе кривая стремится к замкнутой геодезической (возможно, тривиальной). Процесс устроен как чередование двух фаз. Вначале фиксируем натуральную параметризацию на кривой и выбираем большое $N$, как в предыдущем параграфе, где мы приближали кривую геодезическим многоугольником.

  1. Непрерывно деформируем $\gamma$, как в предыдущем параграфе, в геодезический многоугольник $\gamma’$ на вершинах $\gamma(0), \gamma\left(\frac{1}{N}\right), \ldots, \gamma\left(\frac{N-1}{N}\right)$.
  2. Непрерывно деформируем $\gamma’$, как в предыдущем параграфе, в геодезический многоугольник $\gamma’’$ на вершинах $\gamma’\left(\frac{1/2}{N}\right), \gamma’\left(\frac{3/2}{N}\right), \ldots, \gamma’\left(\frac{N - 1/2}{N}\right)$. Затем заменяем $\gamma$ на $\gamma’’$ и повторяем обе фазы ещё и ещё. Ясно, что длина кривой в этом процессе не увеличивается. Тот факт, что в пределе кривая стремится к замкнутой геодезической, вынесен в задачи).

Набросок доказательства существования нетривиальной замкнутой геодезической на двумерной сфере. Рассмотрим произвольное простое заметание римановой сферы $(S^2, g)$, и начнём стягивать все окружности в нём одновременно при помощи процесса Биркгофа (аккуратно реализованного согласованным образом на всех окружностях одновременно). Все окружности не могут стянуться в точки, потому что их объединение всегда заметает сферу, значит одна из окружностей в пределе станет нетривиальной замкнутой геодезической. \(\square\)

Другая поучительная (морсовская!) версия примерно того же самого доказательства. Фиксируем очень большое $N$ и рассмотрим те простые заметания сферы $(S^2, g)$, в которых все окружности приближаются многоугольниками из $\mathcal{P}_N$. Для каждого заметания выберем окружность максимальной энергии, а затем выберем заметание, в котором этот максимум минимален. Назовём это заметание минимаксным. Окружность максимальной энергии в минимаксном заметании — критическая точка функционала энергии, а значит, замкнутая геодезическая. Её энергия ненулевая, и геодезическая нетривиальна. \(\square\)

Это рассуждение тоже можно адаптировать для непростых заметаний, и это важно в следующем параграфе. Адаптация, принадлежащая Питтсу, Калаби и Цао, гласит, что минимакс для не обязательно простых заметаний достигается либо на замкнутой геодезической (возможно, самопересекающейся), либо на паре замкнутых геодезических.

Теорема Кроука

Если применить рассуждение Биркгофа к аккуратно построенному заметанию, в котором все окружности имеют длину $\le c \cdot \text{area}(S^2,g)$, то мы найдём нетривиальную замкнутую геодезическую длины $\le c \cdot \text{area}(S^2,g)$. В этом параграфе содержится набросок построения такого заметания.

Лемма [Berger]. Пусть $p, q$ — точки на компактном римановом многообразии, расстояние между которыми максимально (и равно диаметру многообразия). Тогда для любого вектора $v \in T_p M$ найдётся кратчайшая геодезическая $\gamma$ между $p$ и $q$ такая, что $\langle \gamma’\vert_p, v \rangle \ge 0$.

Доказательство. Испустим короткий геодезический отрезок $\sigma$ из точки $p$ в направлении $v$: $\sigma(0) = p$, $\sigma’(0) = v$. Проведём кратчайшие геодезические $\gamma_t$ между точками $\sigma(t)$ и $q$ для всех малых $t$ и рассмотрим два случая.

  1. Найдутся сколько угодно малые $t$, для которых угол между $\gamma_t’(0)$ и $\sigma’(t)$ не больше $\pi/2$. Тогда в пределе какая-то подпоследовательность геодезических $\gamma_t$ даст искомую геодезическую между $p$ и $q$.
  2. Для всех $t \le t_0$ этот угол тупой: $\langle \gamma_t’(0), \sigma’(t) \rangle < 0$. Тогда легко убедить себя (строго это следует из “первой вариационной формулы”), что производная расстояния $\text{dist}(\sigma(t), q)$ отрицательна на $[0,t_0]$, что противоречит максимальности расстояния между $p$ и $q$. \(\square\)

Если применить лемму Берже к римановой сфере $(S^2, g)$, то получится соединить диаметрально далёкие точки $x,y \in S^2$ несколькими геодезическими так, что все углы между ними в точках $x$ и $y$ будут не больше $\pi$. Везде далее мы говорим только про риманову сферу $(S^2, g)$ (все остальные рассуждения, кроме леммы Берже, не обобщаются на другие многообразия).

Пусть $\gamma$ — замкнутая несамопересекающаяся кривая на римановой сфере $(S^2, g)$, и пусть $\Omega$ — одна из двух открытых областей, на которые $\gamma$ делит сферу. Будем говорить, что $\gamma$ выпукла по отношению к $\Omega$, если существует $\epsilon > 0$ такое, что для любых двух точек $x, y \in \overline{\Omega}$ на расстоянии $\text{dist}(x,y) < \epsilon$ кратчайшая геодезическая между ними полностью лежит в $\overline{\Omega}$. Перечислим без доказательств ряд простых свойств выпуклых кривых.

  • Если $\gamma = \partial \Omega$ — нетривиальная замкнутая геодезическая, то $\gamma$ выпукла по отношению к $\Omega$.
  • Если $\gamma = \partial \Omega$ — геодезический многоугольник, то $\gamma$ выпукла или невыпукла по отношению к $\Omega$ в зависимости от того, каковы углы в вершинах многоугольника: если все они не больше $\pi$, то выпукла, а если есть угол больше $\pi$, то нет.
  • Если $\gamma$ выпукла по отношению к $\Omega$, то процесс Биркгофа, применённый к $\gamma$, всегда останется внутри $\overline{\Omega}$, и в любой момент кривые в этом процессе будут выпуклы по отношению к той части области $\Omega$, которая не заметена кривыми процесса до этого момента.

Теорема [Croke, 1988].

  1. Существует абсолютная константа $c_1$ такая, что на любой римановой сфере $(S^2,g)$ найдётся нетривиальная замкнутая геодезическая длины не больше $с_1 \text{ diam}(S^2,g)$.
  2. Существует абсолютная константа $c_2$ такая, что на любой римановой сфере $(S^2,g)$ найдётся нетривиальная замкнутая геодезическая длины не больше $с_2 \sqrt{ \text{area}(S^2,g)}$.

Кроук доказал свою теорему с константами $c_1=9, c_2 = 31$ (но он не был ими озабочен и указал, что можно их улучшить). Рассуждение ниже вроде бы приводит к множителям $c_1=6, с_2 = 18$. Лучшие известные константы $c_1 = 4, c_2 = 4\sqrt{2}$ принадлежат Рине Ротман.

Набросок доказательства. Идея доказательства обеих частей теоремы такова. Мы нарисуем на сфере несколько геодезических дуг, которые разрежут сферу на несколько геодезических многоугольников, у которых границы выпуклы (по отношению к ним) и имеют контролируемую длину. Применяя процесс к каждой из этих границ, мы либо найдём замкнутую геодезическую в одной из областей, либо получим заметание сферы короткими кривыми. Это заметание нужно аккуратно привести к виду из определения заметания выше (кривые в нём будут иметь длину $\le 6D$ или $\le 18 \sqrt{A}$), и применить аргумент Питтса–Калаби–Цао.

Для первой теоремы, как в обсуждении после леммы Берже, выберем максимально далёкие точки $x, y \in S^2$, $\text{dist}(x,y) = \text{diam}(S^2,g) = D$, и проведём между ними несколько геодезических $\tau_1, \ldots, \tau_n$ длины $D$, чтобы все углы между ними вокруг точек $x,y$ были не больше $\pi$. Если $n=2$, то мы уже нашли замкнутую геодезическую длины $2D$. В общем случае заметим, что эти геодезические разрезают сферу на области так, что все кривые $\tau_i \cup (-\tau_{i+1})$ (нумерация циклическая) выпуклы по отношению к соответствующим областям, и можно применить аргумент выше (процесс Биркгофа выдаст либо замкнутую геодезическую, либо заметание, к которому нужно применить минимаксный аргумент).

Для второй теоремы тоже начнём с выбора максимально далёких точек $x, y \in S^2$, $\text{dist}(x,y) = \text{diam}(S^2,g) = D$, и проведём между ними кратчайшую геодезическую $\tau: [0,D] \to S^2$, параметризованную длиной дуги. Обозначим $A = \text{area}(S^2,g)$. Если $6D \le 12 \sqrt{A}$, то теорема 1 влечёт результат, так что далее считаем, что $D > 2 \sqrt{A}$. Для произвольного $t \in (\sqrt{A}, D - \sqrt{A})$ рассмотрим точку $w = \tau(t)$ и докажем, что можно через неё провести петлю, разделяющую $x$ и $y$ (они окажутся в разных компонентах дополнения петли) и имеющую длину $\le 2\sqrt{A}$. Для это рассмотрим метрические сферы $S_r(x)$ с центром в $x$ и радиусом $r \in (t - \sqrt{A}, t + \sqrt{A})$, и найдём короткую при помощи неравенства коплощади:

\[\int_{t - \sqrt{A}}^{t + \sqrt{A}} \text{len } S_r(x) \; dr \le A = \int_{t - \sqrt{A}}^{t + \sqrt{A}} (2\sqrt{A} - 2|r-t|) \; dr.\]

Значит, найдётся сфера $S_r(x)$ такая, что её компонента, проходящая через $\tau(r)$, имеет длину $\le 2\sqrt{A} - 2|r-t|$. Объединяя эту компоненту с двукратным обходом отрезка $\tau$ между $\tau(r)$ и $\tau(t)$, получим искомую петлю через $w$ длины $\le 2\sqrt{A}$. Рассмотрим кратчайшую из петель через $w$, разделяющих $x$ и $y$, её длина также $\le 2\sqrt{A}$; она может быть не единственна. Она должна быть несамопересекающейся геодезической петлёй (геодезическим многоугольником с единственной вершиной $w$), и в зависимости от угла при $w$ она должна быть выпукла по отношению к одной из двух областей (содержащей $x$ или $y$), или к обеим сразу (в этом случае она оказывается искомой замкнутой геодезической). Определим относительно замкнутые множества $L,R \subset (\sqrt{A}, D - \sqrt{A})$ так: $t \in L$, если существует кратчайшая геодезическая петля $\gamma_t$ через $\tau(t)$, выпуклая по отношению к области, содержащей $x$; $t \in R$, если существует кратчайшая геодезическая петля $\gamma_t$ через $\tau(t)$, выпуклая по отношению к области, содержащей $y$. Множества $L, R$ покрывают $(\sqrt{A}, D - \sqrt{A})$, и потому возможны лишь следующие ситуации.

  1. Найдётся $t \in L \cap R$. Тогда либо через $\tau(t)$ можно провести геодезическую петлю, выпуклую по отношению к обеим областям (и она оказывается геодезической), либо через $\tau(t)$ можно провести две геодезические петли одинаковой длины, одна выпукла по отношению к области, содержащей $x$, а другая — по отношению к области, содержащей $y$. Можно проверить, что они не пересекаются кроме как в $\tau(t)$, и делят сферу на три области, границы которых выпуклы и имеют длину $\le 4\sqrt{A}$. Можно применить аргумент выше: либо процесс Биркгофа выдаст замкнутую геодезическую, либо заметание, к которому можно применить минимаксный аргумент.
  2. $L$ и $R$ не пересекаются, тогда из относительной замкнутости следует, что одно из них пусто, например $L = \varnothing$. Построим геодезическую петлю $\gamma_{\sqrt{A}}$ длины $\le 2\sqrt{A}$ через $\tau(\sqrt{A})$ как предел петель $\gamma_t$ при $t \to \sqrt{A}$. Предельная петля тоже выпукла по отношению к области, содержащей $y$. Пользуясь леммой Берже, испустим из $x$ в $y$ ещё одну или две геодезические, помимо $\tau$, чтобы они образовывали веер вокруг $x$ из углов $\le \pi$. Петля $\gamma_{\sqrt{A}}$ вместе с двумя или тремя геодезическими отрезками из $x$ до пересечений с $\gamma_{\sqrt{A}}$ в сумме разрезают сферу на три или четыре области с выпуклыми границами длины $\le 6\sqrt{A}$. Как и раньше, либо процесс Биркгофа выдаст замкнутую геодезическую, либо заметание, которое нужно будет модифицировать, чтобы его слои стали объединением окружностей и восьмёрок длины $\le 18\sqrt{A}$, и к нему уже применить минимаксный аргумент. \(\square\)

Все компактные двумерные многообразия, кроме сферы — существенные (задача 8.2), и их систолу мы уже умеем оценивать. Таким образом, все обсуждения последних лекций влекут теорему, заявленную в тизере: на любом компактном двумерном римановом многообразии существует замкнутая геодезическая длины не больше корня из площади (с точностью до абсолютного множителя).

Cсылки