Доказательство и приложения теоремы Кёбе

24 Feb 2023

Доказательство теоремы Кёбе

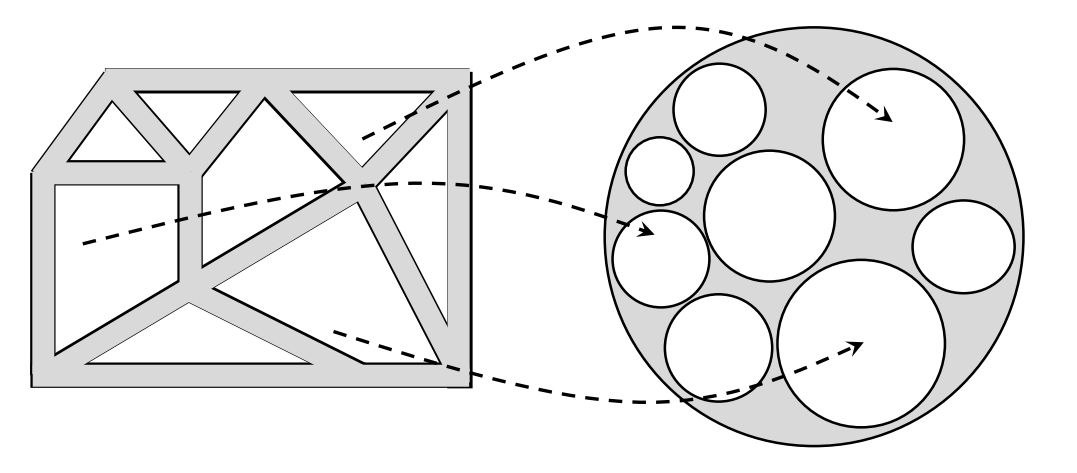
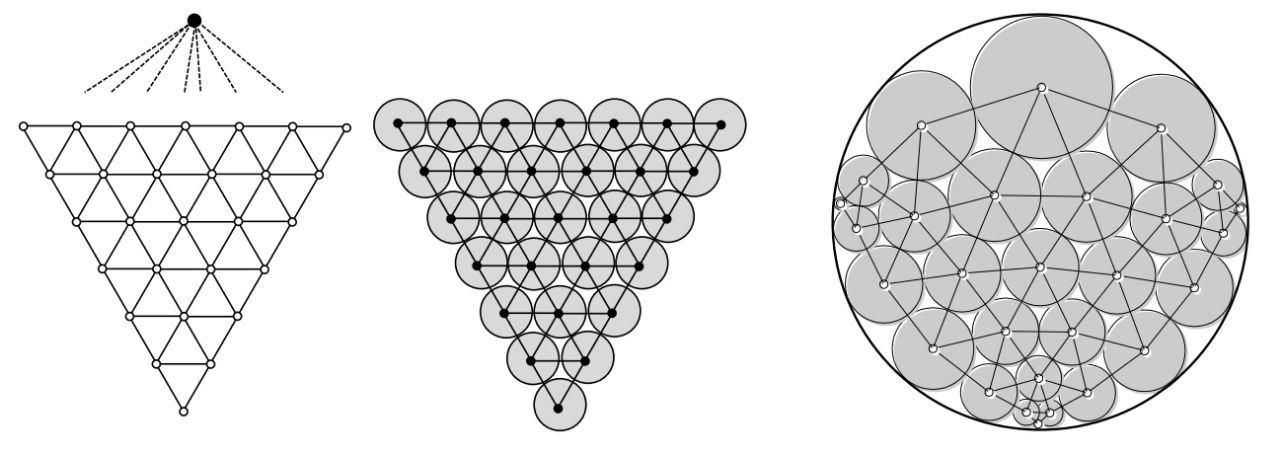
Теорема [Koebe, 1936]. Любой планарный трёхсвязный граф $G = (V,E)$ допускает двойное представление кругами.

Будем считать, что у графа есть треугольная грань $abc$ (иначе заменим $G$ на двойственный граф $G^*$, см. задачу 2). Попробуем организовать двойное представление кругами, чтобы внешней гранью $p_{ext} \in V^*$ оказался треугольник $abc$, причём нарисованный равносторонним образом. Напомню, какой конструкции мы хотим добиться. Это семейство неперекрывающихся кругов $C_i$, $i \in V$, и семейство неперекрывающихся кругов $D_p$, $p \in V^* \setminus p_{ext}$, у которых радиусы $r_u > 0$, $U = V \cup (V^* \setminus P_{ext})$, удовлетворяют следующим соотношениям. Если определить углы

\[\begin{equation} \alpha_{ip} = \arctg \frac{r_p}{r_i}, \quad \alpha_{pi} = \arctg \frac{r_i}{r_p} = \frac{\pi}{2} - \alpha_{ip}, \tag{$\star$} \end{equation}\]

то выполняются равенства

\[\begin{equation} \begin{split} \forall i \in V \setminus \{a,b,c\}: \quad &\sum_{p \text{ инцид. } i} \alpha_{ip} = \pi, \\ \forall i \in \{a,b,c\}: \quad &\sum_{p \text{ инцид. } i} \alpha_{ip} = \pi/6, \\ \forall p \in V^* \setminus P_{ext}: \quad &\sum_{i \text{ инцид. } p} \alpha_{pi} = \pi. \tag{$\heartsuit$} \end{split} \end{equation}\]

Если подобрать радиусы, чтобы для определяемых формулами $(\star)$ углов выполнялись соотношения типа $(\heartsuit)$, то из кругов соответствующих радиусов можно будет собрать искомое двойное представление.

Углы $\beta_{ip} = \pi/2 - \beta_{pi} \in (0,\pi/2)$, удовлетворяющие соотношениям $(\heartsuit)$ (но не обязательно происходящие из каких-то радиусов как в $(\star)$), существуют (задача 2).

Доказательство теоремы Кёбе [Colin de Verdière, 1991]. Рассмотрим вспомогательную функцию $\phi : \mathbb{R} \to \mathbb{R}$: \(\phi(x) = \int_{-\infty}^x \arctg e^t \; dt.\) Она гладкая, возрастающая, выпуклая, и ограничена снизу функцией $\frac{\pi}{2} |x|_{+}$. Здесь мы ввели обозначение положительной срезки

\[|x|_+ = \begin{cases} x, & x\ge 0, \\ 0, & x<0. \end{cases}\]

Аналогично вводится отрицательная срезка, так чтобы выполнялось $|x| = |x|_+ - |x|_-$.

Ключевая идея: исследовать на минимум гладкую функцию $\Phi: \mathbb{R}^U \to \mathbb{R}$,

\[\Phi(x) = \sum_{ip \in J} (\phi(x_p - x_i) - \beta_{ip}(x_p-x_i)),\]

где $J$ обозначает множество всех инцидентных пар $i \in V, p \in V^* \setminus P_{ext}$. Если одновременно увеличить или уменьшить все $x_u$, значение $\Phi(x)$ не поменяется. Если зафиксировать $x_a=0$, и устремить $x$ к бесконечности, то значение $\Phi(x)$ тоже будет стремиться к бесконечности, как следует из оценки

\[\begin{align*} \Phi(x) &= \sum_{ip \in J} (\phi(x_p - x_i) - \beta_{ip}(x_p-x_i)) \\ &\ge \sum_{ip \in J} (\frac{\pi}{2}|x_p - x_i|_+ - \beta_{ip}(|x_p-x_i|_+ - |x_p-x_i|_-)) \\ &= \sum_{ip \in J} (\beta_{pi}|x_p-x_i|_+ + \beta_{ip}|x_p-x_i|_-) \\ &\ge \sum_{ip \in J} \min(\beta_{pi}, \beta_{ip}) |x_p-x_i|. \end{align*}\]

Значит, в какой-то точке $y \in \mathbb{R}^U$ достигается минимум функции $\Phi$. Положим $r_i = e^{y_i}$, $\alpha_{ip} = \arctg \frac{r_p}{r_i} = \arctg e^{y_p-y_i}$, $\alpha_{pi} = \arctg e^{y_i-y_p}$, и проверим, что дают условия первого порядка $\frac{\partial \Phi}{\partial x_u} = 0$. Например, дифференцирование по $x_i$ даёт

\[\sum_{p \text{ инцид. } i} \beta_{ip} = \sum_{p \text{ инцид. } i} \phi'(y_p-y_i) = \sum_{p \text{ инцид. } i} \arctg e^{y_p-y_i} = \sum_{p \text{ инцид. } i} \alpha_{ip},\]

и аналогично можно продифференцировать по $x_p$. Углы $\beta_{\bullet}$ удовлетворяют условиям $(\heartsuit)$, а значит, и углы $\alpha_{\bullet}$ тоже им удовлетворяют. \(\square\)

Приложения теоремы Кёбе

  1. Планарные графы — плохие экспандеры. Мы уже рассмотрели одну манифестацию этого в виде теоремы Липтона–Тарьяна, но есть и более точные утверждения про собственные значеняи лапласиана планарного графа, выводимые из теоремы Кёбе.

  2. Двойное представление графа кругами на сфере легко превращается в трёхмерный гиперболический многогранник с бесконечно удалёнными вершинами и прямыми двугранными углами [Andreev, 1970]. Другое многогранное представление Андреева содержится в задаче 3.

  3. Из графовой теоремы Кёбе можно вывести униформизационную [Rodin–Sullivan, 1987] (и обратно).

    Теорема [Koebe, 1936]. Любая связная открытая область на сфере с границей из конечного числа связных комнонент конформно эквивалентна сфере, из которой выбросили конечное число сферических шапочек и точек.

Конформная теорема Кёбе влечёт графовую Графовая теорема Кёбе влечёт конформную

Cсылки