Гладкие многообразия
Многообразием размерности $n$ называется хаусдорфово топологическое пространство, локально гомеоморфное $\mathbb{R}^n$. Неформально поясню эти слова.
- Топологическое пространство — множество точек, в котором некоторые подмножества некоторым осмысленным образом объявлены открытыми; это позволяет определить у каждой точки её открытые окрестности. Между топологическими пространствами можно рассматривать непрерывные отображения.
- Хаусдорфовость означает, что у любых двух точек есть непересекающиеся окрестности.
- “Локально гомеоморфное $\mathbb{R}^n$” значит, что у каждой точки есть окрестность, гомеоморфная открытому множеству в $\mathbb{R}^n$. Гомеоморфизм — это непрерывное биективное отображение, обратное к которому тоже непрерывно.
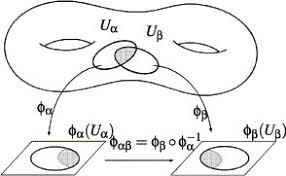
Чтобы многообразие $M^n$ стало гладким, нужно ввести на нём атлас, то есть следующий набор данных.
- $M = \bigcup\limits_{i} U_i$ — открытое покрытие (скажем, счётное).
- $\phi_i : U_i \to \Omega_i \subset \mathbb{R}^n$ — гомеоморфизмы, называемые координатными картами.
- Отображения склейки карт $\phi_j \circ \phi_i^{-1} : \phi_i(U_i \cap U_j) \to \phi_j(U_i \cap U_j)$ — гладкие (скажем, бесконечно дифференцируемые).
Кривая $\gamma : [a,b] \to M$ называется гладкой, если верно следующее. Для любой её точки $\gamma(t)$ рассмотрии карту $U \overset{\phi}\to \Omega \subset \mathbb{R}^n$, в которой точка $\gamma(t)$ лежит вместе со своей окрестностью, то есть $\gamma : (t-\epsilon, t+\epsilon) \to U$. Тогда композиция $\phi \circ \gamma: (t-\epsilon, t+\epsilon) \to \Omega \subset \mathbb{R}^n$ должна быть гладкой.
Касательным вектором в точке $p$ к многообразию $M$ называется класс эквивалентности кривых $\gamma: [0,1] \to M$, $\gamma(0) = p$, по модулю такого отношения эквивалентности: $\gamma_1 \sim \gamma_2$, если $(\phi \circ \gamma_1)’(0) = (\phi \circ \gamma_2)’(0)$ (здесь $U \overset{\phi}\to \Omega$ — карта, содержащая $p$). Все касательные вектора в точке $p$ к многообразию $M$ образуют $n$-мерное векторное пространство, называемое касательным пространством $T_pM$.
Функция $h: M \to \mathbb{R}$ называется гладкой, если для любой карты $U \overset{\phi}\to \Omega \subset \mathbb{R}^n$ композиция $h \circ \phi^{-1} : \Omega \to \mathbb{R}$ есть гладкая функция.
Отображение между многообразиями $f : M \to N$ называется гладким, если верно следующее. Для любой точки $p \in M$ рассмотрим карту $U \overset{\phi}\to \Omega_U$, содержащую $p$, и карту $V \overset{\psi}\to \Omega_V$, содержащую $f(p)$. Тогда композиция $\psi \circ f \circ \phi^{-1}: \phi(U) \to \psi(V)$ должна быть гладкой.
Гладкое отображение $f : M \to N$ индуцирует линейные отображения $df_p : T_pM \to T_{f(p)}N$ для каждой точки $p \in M$. В частности, координатное отображение $\phi : U \to \Omega \subset \mathbb{R}^n$ индуцирует изоморфизмы $d\phi_p : T_pM \to \mathbb{R}^n$ для всех $p \in U$, и их можно использовать, чтобы перетянуть стандартный базис в $\mathbb{R}^n$ в координатные базисы во всех касательных пространствах $T_pM$, $p \in U$. Это позволяет работать в локальных координатах в касательных пространствах.
Римановы многообразия
Римановой метрикой на гладком многообразии $M^n$ называется семейство положительно определённых квадратичных форм $g_p : T_pM \times T_pM \to \mathbb{R}$, гладко зависящих от $p \in M$ в следующем смысле. Пусть есть локальные координаты $\phi : U \to \Omega \subset \mathbb{R}^n$, определяющие базисы $\left(\frac{\partial}{\partial x^i}\right)$ в касательных пространствах $T_pM$, $p \in U$. Тогда для любых $u,v \in T_pM$ имеем:
\[g_p(u,v) = g_p\left( \sum_i u^i \frac{\partial}{\partial x^i}, \sum_j v^j \frac{\partial}{\partial x^j} \right) = \sum_{i,j} g_p\left(\frac{\partial}{\partial x^i},\frac{\partial}{\partial x^j} \right) u^i v^j.\]Так вот, матричные элементы $g_p\left(\frac{\partial}{\partial x^i},\frac{\partial}{\partial x^j} \right)$ должны гладко зависеть от $p$.
Риманово многообразие — гладкое многообразие с римановой метрикой.
Длина кривой $\gamma : [a,b] \to M$ на римановом многообразии определяется как
\[\text{len } \gamma = \int_a^b \sqrt{g_{\gamma(t)}(\dot\gamma(t), \dot\gamma(t))} dt.\]Расстоянием между двумя точками на связном римановом многообразии называется инфимум длин кривых, соединяющих эти точки.
Объём карты $U \overset{\phi}\to \Omega$ на римановом многообразии определяется как
\[\text{vol } U = \int_{\Omega} \sqrt{\det g_{\phi^{-1}(x)}} dx_1 \dots dx_n.\]Интеграл борелевской функции $h: M \to \mathbb{R}$, у которой носитель целиком содержится в карте $U \overset{\phi}\to \Omega$, определяется как
\[\int_M h = \int_{\Omega} h \circ \phi^{-1}(x) \sqrt{\det g_{\phi^{-1}(x)}} dx_1 \dots dx_n.\]Риманов объём оказывается согласован с мерой Хаусдорфа: $\text{vol } U = \frac{\omega_n}{2^n} \mathcal{H}_n(U)$. Здесь $\omega_n$ обозначает объём единичного евклидова шара размерности $n$, а $d$-мерная мера Хаусдорфа определяется так:
\[\mathcal{H}_d(X) = \varliminf_{\epsilon \to 0} \left\{ \sum_i (\text{diam } C_i)^d \middle\vert \begin{array}{l} X \subset \bigcup_i C_i\\ C_i \text{ замкнуты} \\ \text{diam } C_i < \epsilon ~ \forall i \end{array} \right\}.\]Можно проверить, что одномерная мера Хаусдорфа совпадает с длиной. Промежуточные $d$-мерные меры Хаусдорфа для $1 < d < n$ можно использовать, чтобы определить $d$-мерные объёмы как $\frac{\omega_d}{2^d} \mathcal{H}_d(\cdot)$.
Cсылки
- S. Gallot, D. Hulin, J. Lafontaine, Riemannian geometry. Springer (2004).