Разбиения зонотопов

• Видео
• Доска

—Тезисы—

Высотой перестановки $\sigma \in S_n$ назовём число её инверсий, то есть пар $i<j$ таких, что $\sigma(i) > \sigma(j)$. Если $w$ и $w’$ отличаются домножением на одну простую транспозицию справа, то в зависимости от того, у какой из них высота больше, мы пишем либо $w < w’$, либо $w’ < w$. Транзитивное замыкание этого отношения есть (слабый) порядок Брюа на перестановках.

Проводная диаграмма перестановки $\sigma \in S_n$ — то же самое, что представление $\sigma$ в виде кратчайшего произведения простых транспозиций (длины равной числу инверсий), с точностью до перестановки коммутирующих сомножителей. Другими словами, проводная диаграмма — это цепочка перестановок в порядке Брюа $\mbox{id} < \ldots < \sigma$ с точностью до коммутационных соотношений. Флип проводной диаграммы — кокстеровский, то есть замена $s_i s_{i+1} s_i \leftrightarrow s_{i+1} s_i s_{i+1}$.

Проводные диаграммы самой высокой перестановки $\sigma(i) = n+1-i$ отождествляются в замощениями правильного $2n$-угольника ромбами. Флипы диаграмм соответствуют переключениями между двумя способами замостить шестиугольник (про них удобно думать как про изображения трёх верхних или трёх нижних граней куба, спроецированного в шестиугольник).

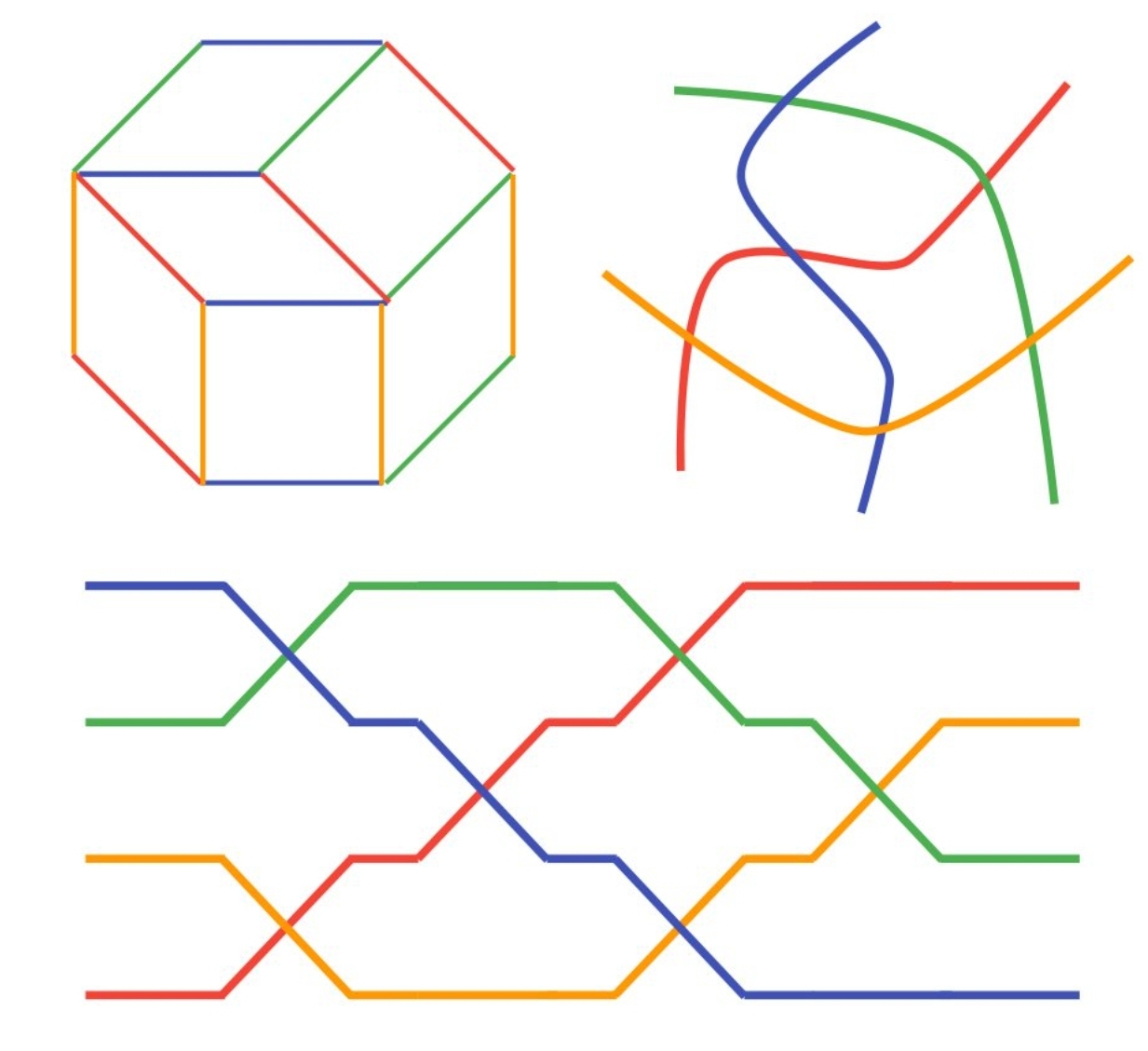
Замощения многоугольника ромбами обобщаются на старшие размерности как зонотопальные разбиения. Зонотоп $Z_V \subset \mathbb{R}^d$, построенный по системе векторов $V = \{v_1, \ldots, v_n\} \subset \mathbb{R}^d$ общего положения (любые $d$ линейно независимы), есть сумма Минковского отрезков $[0,v_i]$. Иными словами, если определить линейную проекцию $p : \mathbb{R}^n \to \mathbb{R}^d$, переводящую $i$-й базисный вектор в $v_i$, то $Z_V = p([0,1]^n)$. Поэтому говорят, что зонотоп — аффинный образ куба. Зонотоп $Z_V$ разбивается (многими способами) на параллелепипеды, представляемые как сумма $d$ отрезков, взятых среди $[0,v_i]$. Заметим что грани куба $[0,1]^n$ нумеруются тройками $X^+ \sqcup X^- \sqcup X^0 = [n]$, которые мы называем знаковыми множествами, через уравнения $x_i = 0$, если $i \in X^-$; $x_i = 1$, если $i \in X^+$; $x_i \in [0,1]$, если $i \in X^0$. Тайлом, отвечающим знаковому множеству $X = (X^+, X^-, X^0)$ назовём образ соответствующей грани под действием $p$: $$\tau_X = \sum_{i \in X^+} v_i + \sum_{i \in X^0} [0,v_i].$$

Набор тайлов $\tau_X$, $X \in T$, образует зонотопальное разбиение $Z_V$, если

• $Z_V = \bigcup\limits_{X \in T} \tau_X$;
• если тайлы $\tau_X$ и $\tau_Y$ пересекаются, то их пересечение — тоже тайл, порождённый знаковым множеством $(X^+ \cup Y^+, X^- \cup Y^-, X^0 \cap Y^0)$, то есть пересечением соответствующих граней куба $[0,1]^n$.

Если дополнительно выполнено $|X^0| \le d$ для всех $X \in T$, то разбиение мелкое (по сути, разрезание на параллелепипеды). Более концептуальное определение мелкого разбиения: это $d$-мерный комплекс $Q \subset [0,1]^n$, который гомеоморфно проецируется на $Z_V$ отображением $p$.

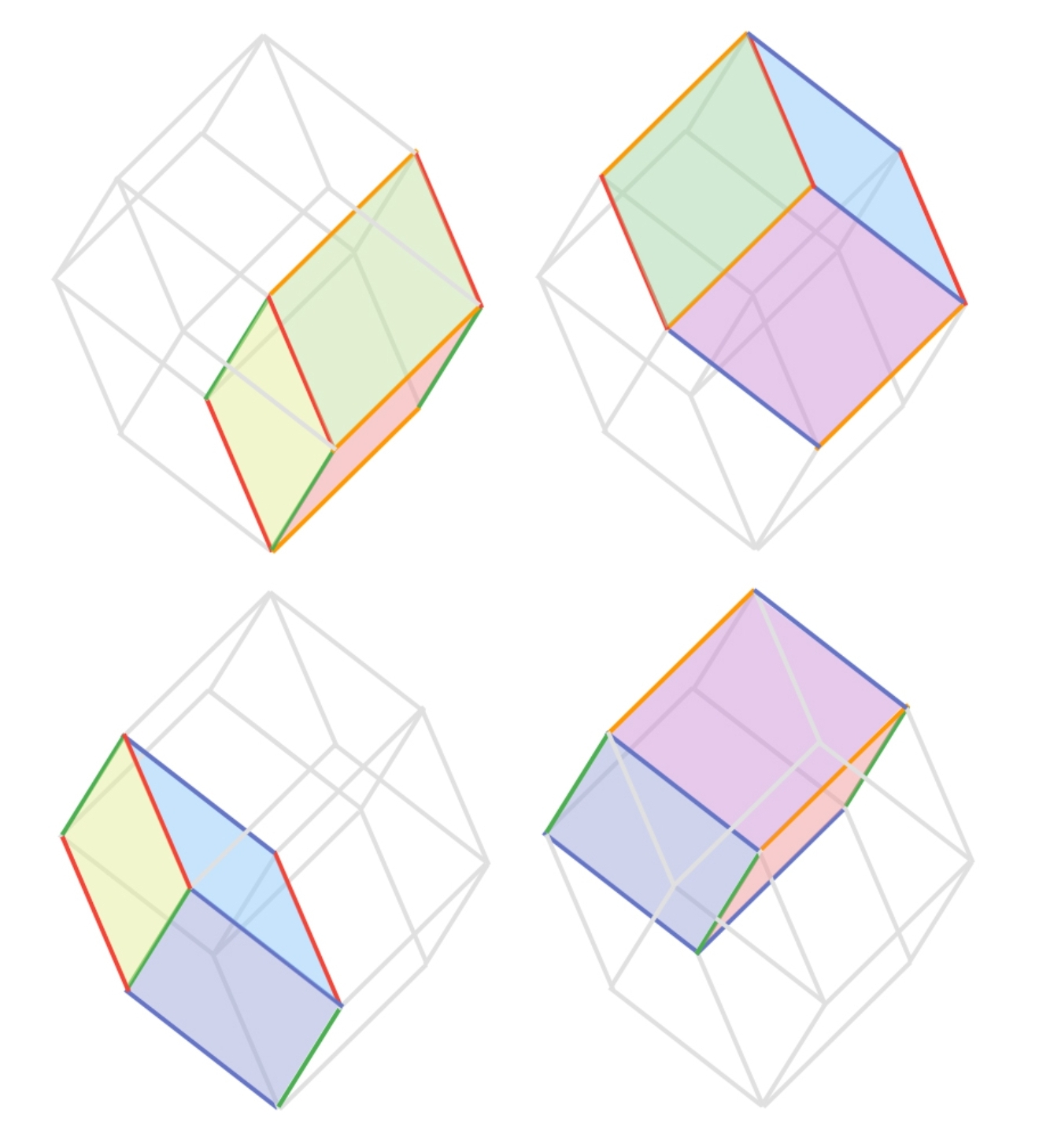
Лемма. Для любого мелкого разбиения $T$ и любого $X^0 \subset [n]$, $|X^0| = d$, в разбиении присутствует тайл “направления” $X^0$.

Набросок доказательства. Если нет, то можно проткнуть куб $(n-d)$-мерным подпространством $L$, ортогональным граням направления $X^0$. Оно не пересекает $Q$, хотя должно, потому что зацеплено с $p^{-1}(\partial Z_V)$, а $Q$ — топологический $d$-диск, натянутый на сферу $p^{-1}(\partial Z_V)$. $\square$

Флипы на множестве мелких зонотопальных разбиений $Z_V$ определяются следующим образом. Рассмотрим комплексы $Q$ и $Q’$, которые гомеоморфно проецируются на $Z_V$, и предположим, что их $\mathbb{Z}/2$-сумма (симметрическая разность) ограничивает $(d+1)$-мерный кубик в $[0,1]^n$. Тогда соответствующие разбиения отличаются флипом. Геометрически это выглядит так: $(d+1)$-куб проецируется в некий многогранник внутри $Z_V$ (шестиугольник при $d=2$, ромбододекаэдр при $d=3$), который разбивается на параллелепипеды ровно двумя способами; переход между ними и есть флип.

—Cсылки—

• Очень простой и наглядный пост про зонотопы (и реклама курса А. Постникова в MIT).
• G. Ziegler, Lectures on polytopes. Springer (2012).