—Тезисы—

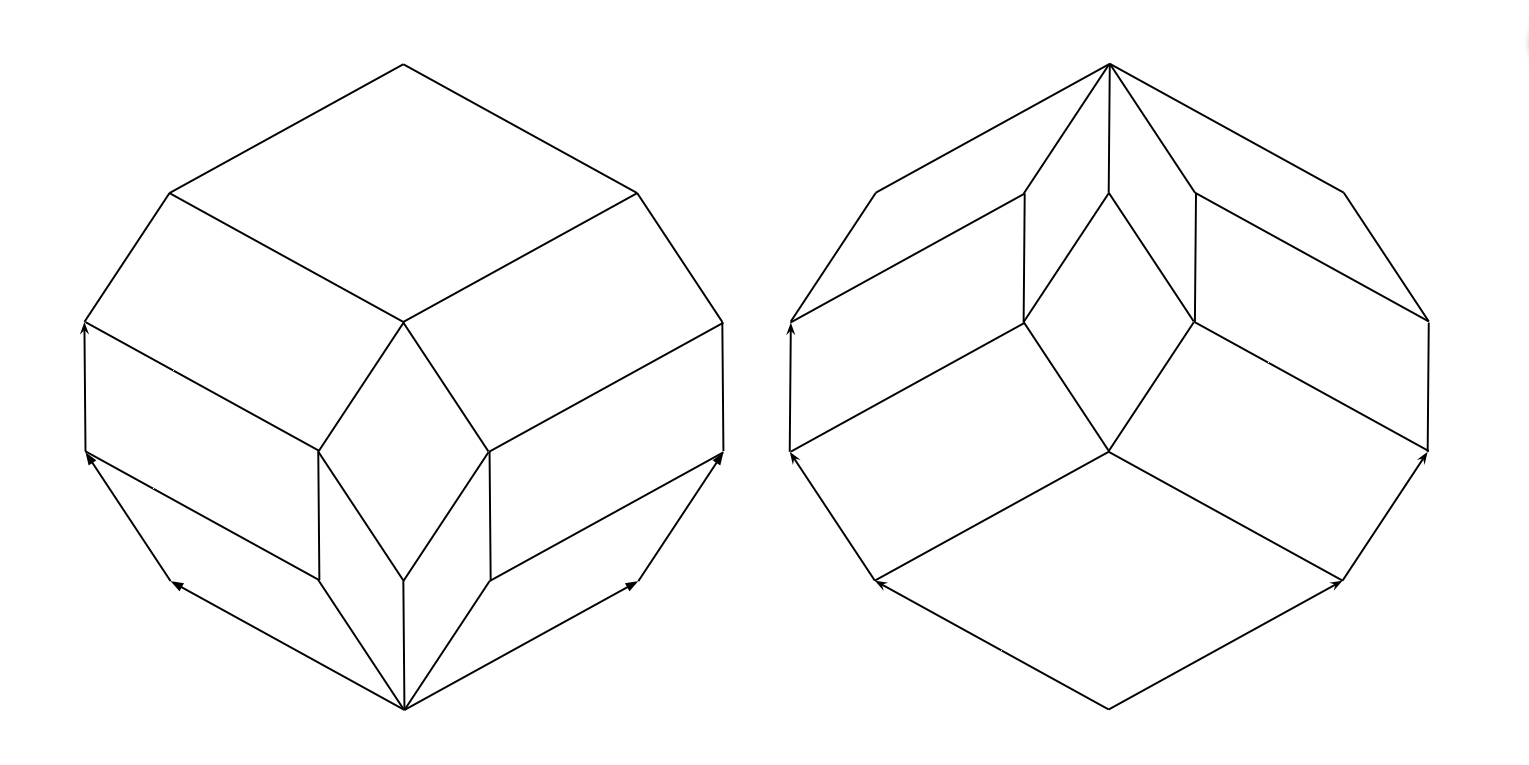
Циклический зонотоп \(Z_{n,d} \subset \mathbb{R}^d\) определяется как сумма Минковского \(\sum\limits_{i=1}^n[0,v_i]\), где точки \(v_i = (1, t_i, t_i^2, \ldots, t_i^{d-1})\) набраны на кривой моментов, для произвольных фиксированных параметров \(t_1 < \ldots < t_n\). Естественная проекция \(Z_{d+1, d+1} \to Z_{d+1, d}\) (“забывающая” последнюю координату) определяет два способа мелко замостить \(Z_{d+1, d}\); для это нужно посмотреть на параллелепипед \(Z_{d+1, d+1}\) из точки с очень положительной или очень отрицательной \((d+1)\)-й координатой; набор видимых граней определяет замощение \(Z_{d+1, d}\). Переключение между двумя этим способами — флип с естественной ориентацией. Ориентированный флип произвольного мелкого зонотопального разбиения \(Z_{n,d}\) получается, если найти внутри этого разбиения копию \(Z_{d+1, d}\) и осуществить флип в ней.

Высшим порядком Брюа \(\mathcal{B}_{n,d}\) называется частичный порядок на множестве мелких зонотопальных разбиений \(Z_{n,d}\), определяемый ориентированными флипами. Порядок \(\mathcal{B}_{n,1}\) — обычный (слабый) порядок Брюа. Высшие порядки обладают множеством любопытных свойств, которые можно неформально обобщить так: топологическая \(k+1\)-связность внутри порядка \(\mathcal{B}_{n,d}\) соответствует топологической \(k\)-связности внутри порядка \(\mathcal{B}_{n,d+1}\).

Теорема. Высший порядок Брюа \(\mathcal{B}_{n,d}\) имеет единственный минимум и единственный максимум.

Минимум и максимум

Набросок доказательства. По аналогии с высотой перестановки, можно определить высоту зонотопального разбиения \(\mathcal{B}_{n,d}\) как количество инверсий у ассоцированного с разбиением набора ломаных поверхностей. Эти поверхности получаются как естественное обобщение проводных диаграмм: в каждом параллелепипеде надо нарисовать \(d\) сечений, параллельных граням, они образуют размещение ломаных поверхностей. Инверсией называется набор из \(d+1\) таких поверхностей, который ограничивает криволинейный симплекс правильной ориентации: если бы он не содержал внутри себя кусков других поверхностей, то в нём можно было бы провести отрицательный флип. Если же он содержит куски других поверхностей, то внутри этого сиплекса можно найти меньший симплекс правильной ориентации (чтобы это строго доказать, достаточно понять устройство этих поверхностей для \(Z_{d+2,d}\); соответствующий флиповый граф есть цикл длины \(2d+4\)). Рассуждая таким образом, можно всегда найти отрицательный флип в разбиении, имеющем хотя бы одну инверсию. Если инверсий нет, то разбиение однозначно восстанавливается. \(\square\)

Высшие порядки Брюа были определены Маниным и Шехтманом иным образом; оригинальное индуктивное определение частично содержится в следующей теореме. Интерпретация через зонотопы принадлежит Г. Циглеру.

Теорема. Множество элементов высшего порядка Брюа \(\mathcal{B}_{n,d+1}\) можно эквивалентно определить так: это цепочки ориентированных флипов в \(\mathcal{B}_{n,d}\) от минимума до максимума, по модулю перестановки коммутирующих флипов.

Набросок доказательства. Внутри разбиения \(Z_{n,d+1}\) можно увидеть множество ломаных поверхностей, которые гомеоморфно проецируются на \(Z_{n,d}\) и дают цепочку разбиений от минимального до максимального. \(\square\)

Теорема. Любой элемент высшего порядка Брюа \(\mathcal{B}_{n,d}\) можно включить в ориентированную цепочку флипов между минимумом и максимумом, состоящую из \({n \choose d+1}\) флипов. Диаметр флипового графа разбиений \(Z_{n,d+1}\) равен \({n \choose d+1}\).

Набросок доказательства. Из того, что любой элемент \(\mathcal{B}_{n,d}\) можно соединить с минимумом, следует связность флипового графа. Флиповое расстояние между минимумом и максимумом вдоль любого пути равно числу тайлов в разбиении \(Z_{n,d+1}\). Чтобы посчитать это число тайлов, мы можем заметить, что флипы не меняют число тайлов, а в минимальном разбиении тайлов ровно \({n \choose d+1}\). \(\square\)

Теорема [B.–Wellman, 2020]. Соотношения между флипами разбиений \(Z_{n,d}\) таковы: любой цикл из флипов можно разбить на “элементарные” флипы двух типов; это четырёхугольники из коммутирующих флипов, а также \((2d+4)\)-угольники, происходящие из разбиений \(Z_{d+2,d}\).

—Cсылки—