—Тезисы—
Ацтекским диамантом порядка \(n\) назовём клеточную фигуру, вписанную в квадрат \(2n \times 2n\) как на рисунке.
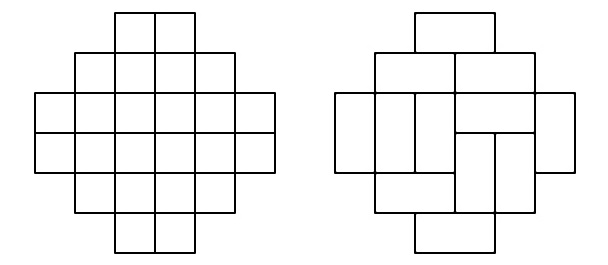
Теорема [Elkies–Kuperberg–Larsen–Propp, 1992]. Количество разбиений ацтекского диаманта порядка \(n\) на доминошки равно \(2^{\frac{n(n+1)}{2}}\).
Доказательство Эу–Фу с лекции использовало трюк Линдстрёма, а также следующие вспомогательные сущности.
Число Шрёдера \(s_n\) определяется как количество путей на плоскости из точки \((0,0)\) в точку \((2n,0)\) вдоль отрезков типа \((1,1), (1,-1), (2,0)\), не опускающихся ниже оси абсцисс.
Число Гиппарха \(h_n\) определяется как количество способов провести несколько диагоналей (возможно, ноль) внутри выпуклого \((n+2)\)-угольника без пересечений во внутренних точках.
Можно показать, что \(s_n = 2h_n\).
—Cсылки—
- Е. Смирнов, Три взгляда на ацтекский бриллиант, МЦНМО (2015).
- N. Elkies, G. Kuperberg, M. Larsen, J. Propp, Alternating-sign matrices and domino tilings: Part I, Part II. Journal of Algebraic Combinatorics (1992).
- S.-P. Eu, T.-S. Fu, [A simple proof of the Aztec diamond theorem]. The Electronic Journal of Combinatorics (2005).
- Видео mathologer’а про замощения доминошками и прорубь внутри диаманта.
- W. Jockusch, J. Propp, P. Shor, Random domino tilings and the arctic circle theorem. Неопубликованный манускрипт (1995).