—Тезисы—
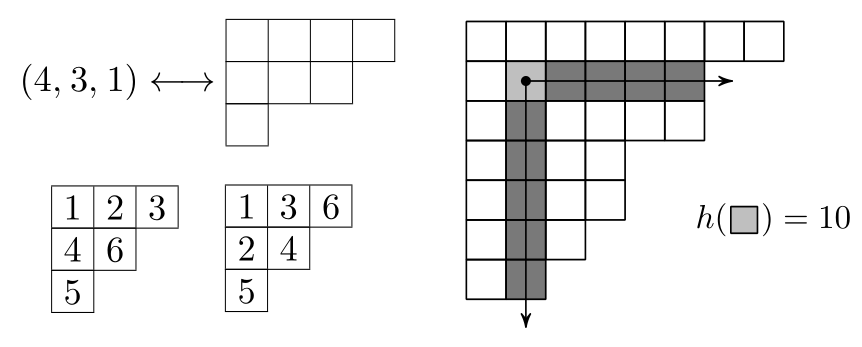
Диаграмма Юнга — разбиение натурального числа в упорядоченную сумму невозрастающих натуральных слагаемых. Диаграмму \(N = \lambda_1 + \ldots + \lambda_k\), \(\lambda_1 \ge \ldots \ge \lambda_k \), обычно изображают квадратиками, так что в строке \(i\) расположено (и выровнено по левому краю) \(\lambda_i\) квадратиков.
Стандартная таблица, соответствующая диаграмме Юнга — расстановка чисел от \(1\) до \(N\) в клетках диаграммы, возрастающая по строкам и по столбцам.
Крюк клетки диаграммы включает в себя саму клетку, все клетки под ней, и все клетки справа от неё; размер крюка \(h(\cdot)\) — количество клеток в крюке.
Формула Фробениуса–Юнга. Количество стандартных таблиц, соответствующих диаграмме Юнга \(\lambda_1 \ge \ldots \ge \lambda_k\), равно \[ \frac{N!}{\ell_1! \cdot \ldots \cdot \ell_k!} \prod_{i < j} (\ell_i - \ell_j), \] где \(\ell_i = \lambda_i +k-i\).
Формула крюков [Frame–Robinson–Thrall, 1954]. Количество стандартных таблиц, соответствующих диаграмме Юнга \(D\), равно \[ \frac{N!}{\prod\limits_{\square \in D} h(\square)}. \]
—Cсылки—
- М. Берштейн, Г. Мерзон, Диаграммы Юнга, пути на решётке и метод отражений. Математическое просвещение (2014).
- Е. Смирнов, Диаграммы Юнга, плоские разбиения и знакочередующиеся матрицы. МЦНМО (2014).
- У. Фултон, Таблицы Юнга и их приложения к теории представлений и геометрии. МЦНМО (2006).
- J. Frame, G. Robinson, R. Thrall, The hook graphs of the symmetric group. Canadian Journal of Mathematics (1954).