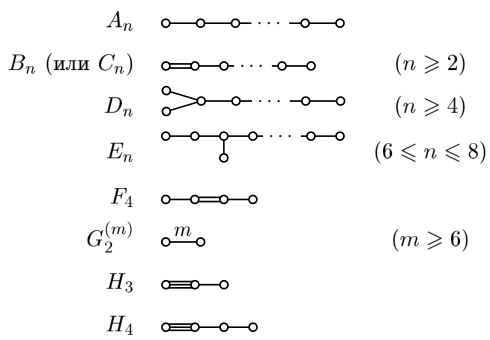—Тезисы—
Теорема. Всевозможные связные схемы Кокстера конечных групп отражений перечислены ниже:
(Двойное ребро обозначает отметку 4, тройное — 5. В строчке с \(G_2^{(m)}\) опечатка, \(m\) может быть также равно пяти, и такую группу можно назвать и \(H_2\)).)
Системы корней (и группы) \(A_n, B_n, D_n\) были описаны ранее. Группы \(G_2^{(m)}\) — диэдральные. Системы корней \(F_4, H_4\) можно построить как прообразы групп вращений куба и икосаэдра при двулистном накрытии \(\operatorname{Sp}(1) \to \operatorname{SO}(3)\), которое представляет вращения через единичные кватернионы. Полученные прообразы в \(\operatorname{Sp}(1)\) оказываются системами корней в четырёхмерном пространстве кватернионов и порождают группы отражений. Группа \(H_3\) — группа симметрий икосаэдра, а также подгруппа в \(H_4\). Группа \(E_8\) соответствует системе корней, состоящей из кратчайших ненулевых векторов решётки \(E_8\) — наименьшей восьмимерной решётки, содержащей вектора из \(\mathbb{Z}^8\) с чётной суммой координат, а также вектор \((\frac12, \frac12, \ldots, \frac12)\). Группы \(E_6\) и \(E_7\) — подгруппы в \(E_8\).
—Cсылки—
- J. Humphreys, Reflection groups and Coxeter groups. Cambridge university press (1990).
- В. Бугаенко, Классификация многогранников Кокстера Математическое просвещение (2003).
- Е. Смирнов, Группы отражений и правильные многогранники. МЦНМО (2018).